Объем фигуры равен 22500 см³.
Пошаговое объяснение:
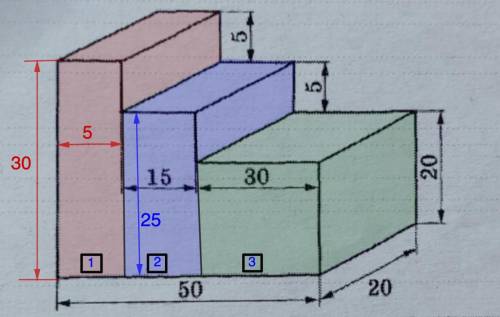
Надо найти объём фигуры, изображённой на рисунке.
Для того, чтобы это сделать, рассмотрим рисунок.
Видим, что фигура состоит из трех параллелепипедов. Поэтому искомый объем будет складываться из объемов этих параллелепипедов:

Объем параллелепипеда равен произведению трех его измерений: длины, ширины, высоты:
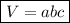 , где а - длина, b - ширина, с - высота.
, где а - длина, b - ширина, с - высота.
1. Найдем объем 3-го параллелепипеда:
а = 30 см; b = 20 см; с = 20 см.

2. Найдем объем 2-го параллелепипеда:
a = 15 см; b = 20 см; с = 20 + 5 = 25 (см).
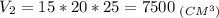
3.Найдем объем 1-го параллелепипеда:
a = 50 - (30 + 15) = 5 (см); b = 20 см; с = 25 + 5 = 30 (см).
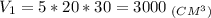
4. Найдем объем фигуры:
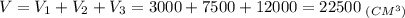
Искомый объем фигуры равен 22500 см³.
12 км/час собственная скорость катера
Пошаговое объяснение:
Пусть х км/час собственная скорость катера, тогда:
х+4 км/ч скорость по течению
х-4 км/ч скорость против течения
За разное время и с разной скоростью катер проплывёт одинаковое расстояние как по течению, так и против течения:
Составим уравнение:
2(х+4) = 4(х-4)
2х+8 = 4х-16
2х-4х = -16-8
-2х = -24
х = -24/(-2)
х = 12 км/час собственная скорость катера
2(12+4) = 4(12-4)
2*16 = 4*8
32 = 32 (км) - за разное время и с разной скоростью катер проплыл одинаковое расстояние как по течению, так и против течения:
Точки пересечения с осью координат X. График функции пересекает ось X при f(x) = 0, значит надо решить уравнение:
(1/2) x²-(1/5)x⁵= 0. Точки пересечения с осью X: Аналитическое решениеx1 = (2^(2/3) *√5) / 2
Численное решениеx1 = 0. x2 = 1.3572088083
Точки пересечения с осью координат Y: График пересекает ось Y, когда x равняется 0:подставляем x = 0 в x^2/2 - x^5/5. 2 5 0 0 -- - -- 2 5 Результат:f(0) = 0Точка:(0, 0)
График функции:
x -3 -2.5 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 2.2 2.5 3
y 53.1 22.656 8.4 2.644 0.7 0.131 0.119 0 0.3 -0.394 -4.4 -7.887 -16.41 -44.1
Точки перегибов Найдем точки перегибов, для этого надо решить уравнение 2 d ---(f(x)) = 0 2 dx (вторая производная равняется нулю),корни полученного уравнения будут точками перегибов для указанного графика функции, 2 d ---(f(x)) = 2 dx 3 1 - 4*x = 0 Решаем это уравнение Корни этого ур-ния 3 ___ \/ 2 x1 = 2 Интервалы выпуклости и вогнутости:Найдём интервалы, где функция выпуклая или вогнутая, для этого посмотрим, как ведет себя функция в точках перегибов:Вогнутая на промежутках 3 ___ \/ 2 (-oo, ] 2 Выпуклая на промежутках 3 ___ \/ 2 [, oo) 2 Горизонтальные асимптоты Горизонтальные асимптоты найдём с пределов данной функции при x->+oo и x->-oo 2 5 x x lim -- - -- = oo x->-oo2 5 значит,горизонтальной асимптоты слева не существует 2 5 x x lim -- - -- = -oo x->oo2 5 значит,горизонтальной асимптоты справа не существует Наклонные асимптоты Наклонную асимптоту можно найти, подсчитав предел функции x^2/2 - x^5/5, делённой на x при x->+oo и x->-oo 2 5 x x -- - -- 2 5 lim = -oo x->-oo x значит,наклонной асимптоты слева не существует 2 5 x x -- - -- 2 5 lim = -oo x->oo x значит,наклонной асимптоты справа не существует Чётность и нечётность функции Проверим функцию чётна или нечётна с соотношений f(x) = f(-x) и f(x) = -f(-x).Итак, проверяем: 2 5 2 5 x x x x -- - -- = -- + -- 2 5 2 5 - Нет 2 5 2 5 x x x x -- - -- = - -- - -- 2 5 2 5 - Нет. значит, функция не является ни чётной ни нечётной.