тут будем решать неравенством
пусть х тетрадь в линейку тогда по условию максимально возможное количество тетрадей в клетку х+9 нам известно что тетрадь в линейку стоит 2 коп а тетрадь в клетку 3 коп тогда стоимость каждого наименования будет 2х и 3(х+9) нам известно что у покупателя 1 руб и 40 коп иначе 140 коп соответственно сумма стоимости наименований не более имеющих денег
получаем
3(х+9)+2х≤140
3х+3×9+2х≤140
3х+27+2х≤140
5х+27≤140
5х≤113
х ∈ (-∞; 22.6]
так как количество может измерятся только в натуральных числах то ищем ближайшее целое число к 22,6 это 22 соответственно 22 тетрадок в линейку ⇒ 22+9=31 тетрадок в клетку
ответ: 22 тетрадок в линейку и 31 тетрадок в клетку
ДАНО: P= 16 см - периметр квадрата ABCD.
НАЙТИ: S(ABC) = ? - площадь треугольника.
РЕШЕНИЕ
Периметр квадрата по формуле:
Р = 4*а = 16 см
Находим сторону квадрата:
а = Р/4 = 16:4 = 4 см - сторона.
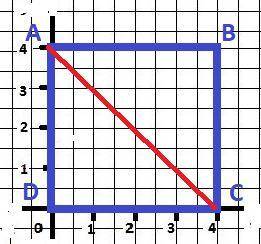
Начертили квадрат - рисунок в приложении.
1 см = 2 клетки в тетради. Обозначили вершины латинскими буквами. Провели диагональ квадрата АС .
ΔАВС = ΔADC - равные по двум сторонам и углу между ними, равнобедренные.
Площадь треугольника по формуле:
S(ABC) = 1/2*a*b = 1/2*a² = 4*4/2 = 8 см² - площадь треугольника - ОТВЕТ
x2 = -3
x3 = -2(5 + √10)
x4 = 2(-5 + √10)