Пошаговое объяснение:
наклонную асимптоту ищем в виде y=ax+b
из определения асимптоты
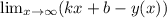
найдем k и b
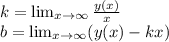
потом найдем точки разрыва и посмотрим их пределы слева и справа
и определим вертикальные асимптоты
итак, с теорией разобрались, поехали с примерами
1)
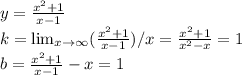
наклонная асимптота у = х + 1
теперь вертикальные
х=1 точка разрыва. смотрим пределы
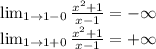
это точка разрыва II рода и вертикальная асимптота х = 1
2)
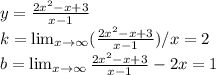
наклонная асимптота у = 2х + 1
теперь вертикальные
х=1 точка разрыва. смотрим пределы
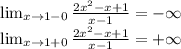
это точка разрыва II рода и вертикальная асимптота х = 1
3)
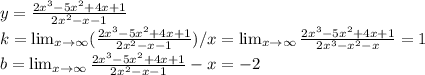
наклонная асимптота у = х - 2
теперь вертикальные
х₁ = - 0.5 точка разрыва. смотрим пределы
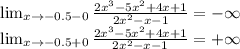
это точка разрыва II рода и вертикальная асимптота х = -0.5
x₂ = 1
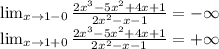
это точка разрыва II рода и вертикальная асимптота х = 1
4)
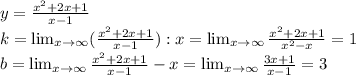
наклонная асимптота у = х + 3
х=1 точка разрыва. смотрим пределы
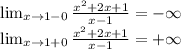
это точка разрыва II рода и вертикальная асимптота х = 1
Пошаговое объяснение:
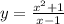
ОДЗ: х-1≠0 х≠1.
1) определим вертикальные асимптоты:
х=1.
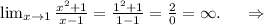
x=1 - вертикальная асимптота.
2) определим наклонные асимптоты:
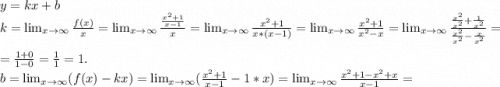
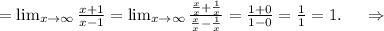
y=x+1 - наклонная асимптота.
ответ: х=1, у=х+1.
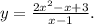
ОДЗ: х-1≠0 х≠1.
1) определим вертикальные асимптоты:
х=1.
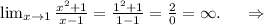
x=1 - вертикальная асимптота.
2) определим наклонные асимптоты:
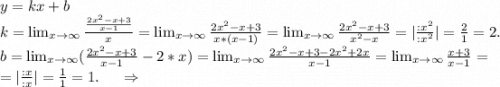
y=2x+1 - наклонная асимптота.
ответ: х=1, у=2х+1.
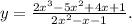
ОДЗ: 2x²-x-1≠0
2x^2-2x+x-1≠0
2x*(x-1)+(x-1)≠0
(x-1)*(2x+1)≠0
x-1≠0
x≠1
2x+1≠0
x≠-0,5.
1) определим вертикальные асимптоты:
x=1.
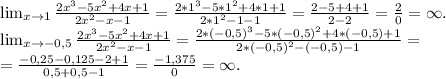
x=1 и х=-0,5 - вертикальные асимптоты.
2) определим наклонные асимптоты:
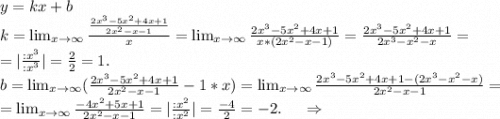
y=x-2.
ответ: x=1, x=-0,5, y=x-2.
Производная функции равна y' = -(x + 1)/(x- 1)³.
Приравняв нулю, получаем критическую точку х = -1.
С учётом того, что функция в точке х = 1 терпит разрыв, имеем 3 промежутка монотонности функции: (-∞; -1), (-1; 1) и (1; +∞).
Находим знаки производной на полученных промежутках.
х = -2 -1 0 1 2
y' = -0,037 0 1 - -3 .
Отсюда получаем ответ: на промежутках (-∞; -1) и (1; +∞) функция убывает, на промежутке (-1; 1) - возрастает.