Пошаговое объяснение:
Проведем перпендикуляры к оси n на диаграмме ( рисунок во вложении) и найдем сколько учеников написали контрольную на
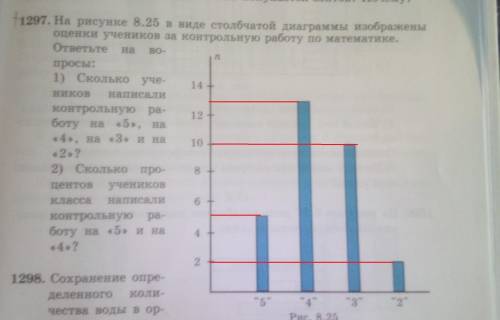
1) оценку 5 - 5 учеников
оценку 4 - 13 учеников
оценку 3 - 10 учеников
оценку 2 - 2 ученика
2) Всего учеников в классе
5+13+10+2= 30 учеников и это 100 %
На оценку 5 написали 5 учеников и это составит
30 уч- 100%
5 уч- х %
х= (5*100)/30=16, (6) ≈17% учеников написали на 5
На оценку 4 написали 13 учеников и это составит
30 уч.- 100%
13 уч. - х %
х= (13*100)/30=43, (3) ≈43 % учеников написали на 4
Пошаговое объяснение:
Проведем перпендикуляры к оси n на диаграмме ( рисунок во вложении) и найдем сколько учеников написали контрольную на
1) оценку 5 - 5 учеников
оценку 4 - 13 учеников
оценку 3 - 10 учеников
оценку 2 - 2 ученика
2) Всего учеников в классе
5+13+10+2= 30 учеников и это 100 %
На оценку 5 написали 5 учеников и это составит
30 уч- 100%
5 уч- х %
х= (5*100)/30=16, (6) ≈17% учеников написали на 5
На оценку 4 написали 13 учеников и это составит
30 уч.- 100%
13 уч. - х %
х= (13*100)/30=43, (3) ≈43 % учеников написали на 4

ответ: 0.3
Пошаговое объяснение:
Найдем вероятность того ,что абонент угадает цифру с первой попытки это P1=1/10 , тк всего 10 цифр ( от 0 до 9)
Найдем вероятность того ,что он угадает цифру со второй попытки:
Вероятность того , что в первый раз абонент не угадает цифру равна: 9/10 , а вероятность того что во второй раз он угадает цифру равна: 1/9
P2=9/10 *1/9=1/10 , тк не угадав цифру в первый раз, цифр остается на одну меньше. (неугаданную цифру абонент исключает из списка подозреваемых)
Аналогично находится вероятность когда он угадает цифру с третьей попытки:
P3=9/10 * 8/9 * 1/8=1/10
Как видим вероятности угадать цифру с любой попытки равны.
Таким образом вероятность угадать цифру не более чем с трех попыток равна: P1+P2+P3=3/10=0.3
ответ: 0.3