1. Заменяем переменную. sqrt(x) = t, x = t^2, dx = 2t dt
Int (e^sqrt(x)) dx = 2*Int (t*e^t) dt.
По частям. u = t, dv = e^t dt, du = dt, v = e^t
2Int (t*e^t) dt = uv - Int v du = 2*(t*e^t - Int e^t dt) = 2*t*e^t - 2*e^t + C = 2*e^t*(t - 1) +C
2. По частям. u = ln(3+x^2), dv = dx, du = 2x / (3+x^2), v = x
Int ln(3+x^2) dx = uv - Int v du = x*ln(3+x^2) - Int 2x^2 / (3+x^2) dx = x*ln(3+x^2) - 2*Int (3+x^2-3) / (3+x^2) dx =
= x*ln(3+x^2) - 2*Int (1 - 3/(3+x^2)) dx = x*ln(3+x^2) - 2x + 6/sqrt(3)*arctg (x/sqrt(3)) + C =
= x*ln(3+x^2) - 2x + 2*sqrt(3)*arctg (x/sqrt(3)) + C
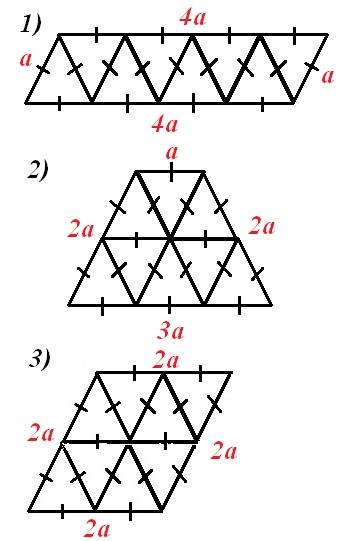
На вскидку сразу смог составить следующие 3 четырехугольника - чертеж во вложении.
Обозначим сторону правильного треугольника через а. В правильном треугольнике все стороны равны и все углы по 60°.
1) Данный четырехугольник - параллелограмм. У него противоположные стороны равны, противолежащие углы равны. Из периметра параллелограмма получим уравнение:
2(а+4а)=16 => a = 1,6 => S параллелограмма = 4a*a*sin60° = (4a²√3)/2 = 2a²√3.
2) Данный четырехугольник - равнобокая трапеция. Из периметра трапеции получим:
а + 2а + 3а + 2а = 16 => a = 2 => S = H(a+3a)/2 = 2aH, где Н - высота трапеции....
Длинц высоты трапеции можно найти как длину высоты равностороннего треугольника со стороной 2а.
По теореме Пифагора: Н² = (2а)² - а² = 3а² => H = a√3
Тогда S трапеции = 2а*a√3 = 2a²√3.
3) Данный четырехугольник - ромб. Его противоположные стороны равны, противоположные углы равны.
4*2а=16 => a = 2 => S ромба = (2а)²sin 60° = 2a²√3.
2.<
3.>
4.=
5.=
6.<
7.=
8.>
9.>
10.=