где a, b, c – стороны треугольника
S – площадь треугольника
Нам неизвестны ни стороны треугольника, ни его площадь. Обозначим катеты как х, тогда гипотенуза будет равна: x√2.
А площадь треугольника будет равна 0,5х².
Значит 2 = (2*0.5x²)/(x+x+x√2) = x²/(x(2+√2)) = x/(2+√2).
Сторона х = 4+2√2.
Таким образом, гипотенуза будет равна: с = (4+2√2)*√2 =
= 4+4√2 = 4(1+√2).
Можно выразить так: с ≈ 4(1+1,414214) ≈ 9,656854.
2) Так как центр вписанной окружности лежит на биссектрисе острого угла, то с = 2*r/(tg(45/2).
tg(45/2) можно взять из таблиц или выразить так:
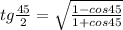 .
.
Результат тот же: с ≈ 9,656854.
1 часть - одна сторона (а)
5 частей - вторая сторона (b)
P = (a + b) * 2
(1 + 5) * 2 = 12 частей - всего
36 : 12 = 3 см - 1 часть, значит :
1 сторона = 3 см
2 сторона = 3 * 5 = 15 см
Проверим : (3 + 15) * 2 = 36 см периметр - верно
S = a * b
3 * 15 = 45 см² - площадь прямоугольника.
б) 1 : 3
(1 + 3) * 2 = 8 частей всего
36 : 8 = 4,5 см - 1 часть (или одна сторона)
4,5 * 3 = 13,5 см - вторая сторона
4,5 * 13,5 = 60,75 см² - площадь
в) 1 : 2
(1 + 2 ) * 2 = 6 частей - всего
36 : 6 = 6 см - 1 сторона
6 * 2 = 12 см - 2 сторона
6 * 12 = 72 см² - площадь
г) 1 : 1
(1 + 1) * 2 = 4 части - всего
36 : 4 = 9 см - каждая сторона, т.к. они равны (квадрат)
9 * 9 = 81 см² - площадь.
Площадь прямоугольников от первого до последнего увеличивается (чем больше соотношением между сторонами - тем меньше площадь).
Самая большая площадь у квадрата.