Дано:
стороны треугольника соотносятся как 2:3:4
P(MNO) = 27 см
Найти: стороны треугольника
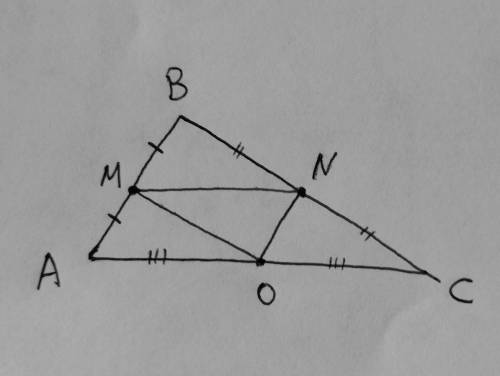
По свойству средней линии треугольника, три средние линии делят исходный треугольник на четыре равных треугольника. Треугольник MNO — серединный. По свойству серединного треугольника следует, что
P(MNO) = (P(ABC)) / 2
Пусть стороны треугольника будут 2х, 3х, 4х соответсвенно.
AB = 2x, BC = 3x, AC = 4x
P(ABC) = AB + BC + AC = 2x + 3x + 4x = 9x
Дано, что P(MNO) = 27 см, значит
27 = (9х) / 2
9х = 54
х = 6, отсюда следует, что стороны треуголника равны
AB = 2x = 12, BC = 3x = 18, AC = 4x = 24
ответ: 12; 18; 24.
2) 5 целых 13/20÷(8 целых1/15 - 3/5) = ...можно решить по действиям
1) 8 целых 1/15 - 3/5 = 8 целых 1/15 - 9/15 = 7 целых 16/15 - 9/15 = 7 целых 7/15
2) 5 целых 13/20 ÷ 7 целых 7/15 = 113/20÷ 112/15 = 113/20× 15/112 = 113×15/20× 112 = 113 ×3/4×112=339/448
ответ: 339/448