Если прямая проходит через точку M (2; -6) и отсекает на осях Ox и Oy отрезки одинаковой длины, то её угловой коэффициент равен 1 (к = Δу/Δх).
Пусть прямая пересекает ось Оу в точке А, ось Ох в точке В.
Проекция отрезка МВ на ось Ох равна 6 единиц (так как по оси Оу координата точки М равна 6 единиц). Итого получаем значение ординаты точки В, равной 2 + 6 = 8.
Так как точка М находится в 4 четверти (отрицательные значения по оси Оу), то по условию задания принимаем 8 единиц вниз от нуля. Это точка А (0; -8).
ответ: уравнение прямой у = х - 8.
X, для которых есть y Y.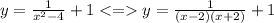
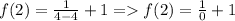
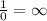следовательно нет такого действительного числа y, которое станет в паре с 2 
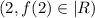, значит 2 не может быть в области определения (с -2 тот-же случай).
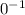не определено, потому "число" 
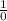не существует, а значит - любой хX который приводит к подобному результату - не имеет смысла, следовательно находится вне области определения.
Мы знаем, что от первого куска отрезали 14 м, а от второго – 22 метра, тогда в 1 куске было (3х+14) м ткани, а во втором было – (х+22) м ткани.
В условии сказано, что ткани изначально было поровну, значит можем составить уравнение:
1) 3х+14=х+22,
2х=8,
х=4 м ткани осталось во втором куске,
2) 4Ч3=12 м ткани осталось в первом куске,
3) 4+22=26 м было в первом куске изначально.
Мы знаем, что в первом и втором кусках ткани было поровну, следовательно, и во втором куске было 26 м ткани.
ответ: первоначально в каждом куске ткани было 26 м