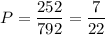Выбрать из 12 деталей 7 можно с выбрать из 9 стандартных деталей 6 стандартных можно с и одну нестандартную из (12-9) трех нестандартных с т.е. выбрать 7 деталей, среди которых 6 стандартных, можно с Искомую вероятность находим с формулы классического определения вероятности m/n=
(3*9!/(6!*3!))/(12!/(7!*5!))=(3*9!*7!*5!)/(6!*3!*12!)=7/(2*11)=7/22
Пошаговое объяснение:
На доске записано три числа
17,20,25
далее Петя на бумажке записывает произведение любых двух, а на доске на 1 уменьшает третье
На доске На бумажке Разница
17*20*25=8500
17*20*24=8160 17*20=340 8500-8160=340
16*20*24=7680 20*24=480 8160-7680=480
16*19*24= 7296 16*24= 384 7680-7296= 384
Как видим , произведение трех чисел на доске уменьшается на произведение чисел записанных на бумажке.Когда одно из чисел станет 0 , произведение их чисел на доске тоже станет 0. Значит сумма всех произведений чисел записанных Петей на бумажке , равна начальному произведению на доске, т.е 17*20*25=8500
В партии 12 - 9 = 3 деталей бракованных
Общее число возможных элементарных исходов для данных испытаний равно числу которыми можно извлечь 7 детали из 12:
Подсчитаем число исходов, благоприятствующих данному событию:
одну деталь среди 3 бракованных можно выбрать количество которых равно: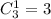 , а шесть деталей среди 9 стандартных можно выбрать
, а шесть деталей среди 9 стандартных можно выбрать 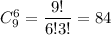 . По правилу произведения, всего благоприятных исходов:
. По правилу произведения, всего благоприятных исходов: 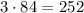
Искомая вероятность: