(это правильно, я тоже Сириус решаю)
Пошаговое объяснение:
Пронумеруем числа 
, 
, 
, ..., 
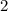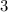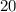
Пусть 
- ая группа состоит из чисел с номерами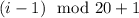 
, 
, 
, ..., 
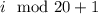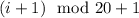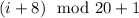(здесь 
- взятие остатка, 
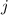- ое число в - ой группе имеет номер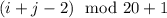 
, 
, 
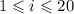). К примеру:
1-ая группа: числа , , ..., 
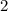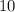
2-ая группа: числа , , ...,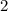 
...
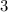20-ая группа: числа , , ...,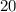 
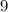
Пусть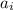 
- сумма чисел в - ой группе. Поскольку все числа целые, их сумма будет также целая, значит, ![\forall i\in[1,~20]](/tpl/images/2025/8085/f00d2.png)
: 
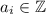. Заметим, что сумма всех чисел является суммой чисел в -ой и в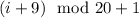 
, значит, 
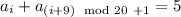. Если 
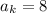, то есть ![\forall i\in [1,~k)\cup(k,20]](/tpl/images/2025/8085/cb834.png)
: 
⇒
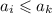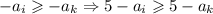. Поскольку 
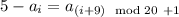и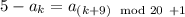 
, постольку 
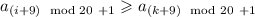. Поэтому 
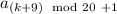- минимальное число (все остальные числа не меньше 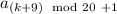(а именно все, потому что в виде 
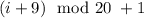представляются все числа от 1 до 20 при ![i\in[1,~20]](/tpl/images/2025/8085/a631f.png)
) ). А также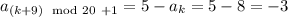 
. В итоге : 
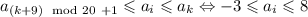. В итоге, поскольку : ![a_i\in \mathbb{Z} ~\wedge~a_i\in[-3,~8]](/tpl/images/2025/8085/54ef8.png)
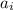, у есть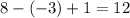 
вариантов значения. Значит, не более 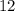сумм различны. Для полноты картины стоило бы привести пример, но это слишком просто.
Условие
Натуральное число умножили последовательно на каждую из его цифр. Получилось 1995. Найдите исходное число.
Подсказка
Разложите число 1995 на простые множители.
Решениена
1995 = 3·5·7·19. Надо разбить это произведение на две группы: часть множителей войдёт в исходное число, а другая часть будет его цифрами. Ясно, что 19 войдёт в искомое число (цифры "19": нет!). Остаётся несложный перебор, который даёт единственный ответ: 57·5·7 = 1995.
ответ
57.
Пошаговое объяснение:
просто подстав замість 1995 3666
Ничего другого в голову не приходит.Раз есть широкий изгиб,значит есть и узкий?