Пошаговое объяснение:
Дано: ΔАВС; ∠АСВ = 90°
АР = АС; ВQ = ВС
Найти: ∠РСQ
Решение.
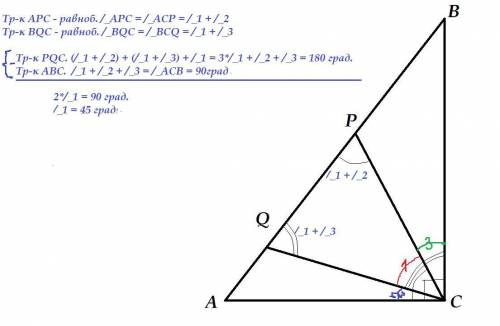
Рассмотрим Δ АВС. Отрезки СР и CQ делят прямой угол на 3 угла. Для удобства назовем ∠1 искомый ∠PCQ , ∠АСQ, прилежащий к стороне АС, ∠2 и ∠ВСР, прилежащий у стороне ВС ∠3.
∠АСВ = ∠1 + ∠2 + ∠3 = 90° (это уравнение пригодится далее)
Рассмотрим ΔАРС, боковые стороны АР=АС по условию, ⇒ равны углы при основании этого равнобедренного треугольника:
∠АРС = ∠АСР = ∠1 + ∠2.
Рассмотрим ΔВQС, он также равнобедренный по условию (BQ = ВС), ⇒ можно записать равенство углов при его основании:
∠ВQC = ∠BCQ = ∠1 + ∠3
Рассмотрим ΔРQС. Сумма его углов, как и любого треугольника, 180 ° :
∠АРС + ∠ВQC + ∠РСQ = (∠1 + ∠2) + (∠1 + ∠3) + ∠1 = 3 *∠1 + ∠2 + ∠3 = 180°
Имеем систему уравнений, которую можно решить вычитания.
{ 3 *∠1 + ∠2 + ∠3 = 180°
{ ∠1 + ∠2 + ∠3 = 90°
2 * ∠1 = 90°
∠1 = 45°
ответ: 45°
Современная лёгкая атлетика начала свой путь с отдельных попыток в разных странах проводить соревнования в беге, прыжках и метаниях. Зафиксированы результаты в прыжке с шестом в 1789 г, в беге на одну милю в 1792 г. и 440 ярдов в 1830 г. в прыжке в высоту в 1827 г, в метании молота в 1838 г, в толкании ядра в 1839 г. ( и др.[источник не указан 1805 дней. Считается, что начало истории современной лёгкой атлетики положили соревнования в беге на дистанцию около 2 км учащиеся колледжа в г. Регби (Великобритания) в 1837 г., после чего такие соревнования стали проводиться в других учебных заведениях Великобритании.
1 1/4-1/3=5/4-1/3=15/12-4/12=11/12
1 13/15-2/5=28/15-2/5=28/15-6/15=22/15=
=1 7/15
1 1/3-5/6=4/3-5/6=8/6-5/6=3/6=1/2
2 3/10-4/15=23/10-4/15=69/30-8/30=61/30=
=2 1/30
3 1/8-1/6=25/8-1/6=75/24-4/24=71/24=2 23/24
1/2×1/2÷1 1/2=1/4÷3/2=1/4×2/3=1/6
25×7/15÷25/27=7/15×25×27/25=63/5=12 3/5
5/9 ×2 1/4÷20=5/9×9/4×1/20=1/16