Решение.
1. Угол ВСО=углу СОД как накрест лежащие при ВС ∥АД и секущей СО
Но угол ВСО=углу ОСД по условию.
Значит, в треугольнике СОД угол СОД=углу ОСД и треугольник ОСД - равнобедренный
ОД=СД=17
2. Угол ВОА=углу ОВС как накрест лежащие при ВС ∥АД и секущей ВО
Но угол ОВС = углу АВО по условию
Значит, в треугольнике АВО углы при основании равны и он - равнобедренный.
АВ=АО=10
3. АД= АО+ОД=10+17=27
4. В прямоугольном треугольнике АВК найдем АК по теореме Пифагора.
АК =корень из ( 10^2-8^2)=6
5. В прямоугольном треугольнике МСД найдем МД по теореме Пифагора
МД = корень из ( 17^2-8^2)=15
6.ВС= АД-АК-МД=27-6-15=6
7.Ищем площадь классически - полусумма оснований на высоту. S АБСД=(6+27 *8)/2=132
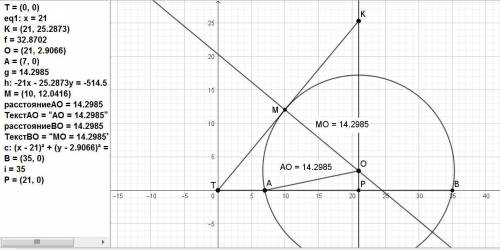
В этой задаче, зная синус угла Т, надо определить его тангенс.
tg T = sin T/√(1 - sin² T) = (√29/7)/(√(1 - (29/49)) = √(29/20).
Центр О окружности находится на прямой х = (7 + 35)/2 = 21.
Примем расстояние точки О от стороны TF, равным у.
Длина отрезка РК (как катета) равна 21*tg T = 21*√(29/20).
Точка М - точка касания окружности с прямой ТЕ, ОМ - радиус R.
Угол МОК равен углу Т как взаимно перпендикулярный.
Отрезок ОК = R/cos T = R/(√(1 - (29/49)) = 7R/√20.
Составим уравнение: РО + ОК = РК. Подставим данные.
у + (7R/√20 = 21*√(29/20),
у*√20 + 7R = 21*√29.
Теперь рассмотрим треугольник ОАР.
R² = (21 - 7)² + y².
Решаем систему с двумя неизвестными R и у.
{y*√20 + 7R = 21*√29.
{R² = (21 - 7)² + y².
Решение системы: R = 77/√29 ≈ 14,2985.
y = 7*√(5/29) ≈ 2,90659.
162945 : d = 3867 - 3654
162945 : d = 213
d = 162945 : 213
d = 765
d : 258 = 35707 : 70
d : 258 = 510,1
d = 510,1 * 258
d = 131605,8
x : 258 = 98756 - 39984
x : 258 = 58772
x = 58772 * 258
x = 15 163 176
(c + 4589) - 5869 = 3216
c + 4589 - 5869 = 3216
c = 3216 + 5869 - 4589
c = 4496