 заявленный и в приведённом условии. Далее порассуждаем практически:
заявленный и в приведённом условии. Далее порассуждаем практически: ;
; ;
;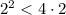 ;
; ;
;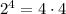 ;
;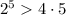 ;
; производная
производная 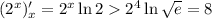 больше производной
больше производной 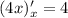 , т.е. дальше левая часть уравнения, растёт быстрее, чем правая, а значит, других корней при
, т.е. дальше левая часть уравнения, растёт быстрее, чем правая, а значит, других корней при  быть не может.
быть не может.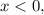 левая часть уравнения положительна, а правая отрицательна, так что других корней при
левая часть уравнения положительна, а правая отрицательна, так что других корней при  быть не может.
быть не может.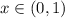 , так как при сравнении двух непрерывных функций на этом интервале меняется знак.
, так как при сравнении двух непрерывных функций на этом интервале меняется знак.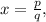 где
где 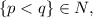 то:
то: ![2^x = 2^\frac{p}{q} = (\sqrt[q]2)^p < 2 .](/tpl/images/0486/4079/dd2eb.png) Это число, очевидно иррационально, что легко доказать от обратного методом Евклида. Однако справа должно быть рациональное число
Это число, очевидно иррационально, что легко доказать от обратного методом Евклида. Однако справа должно быть рациональное число 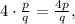 а значит, мы пришли к противоречию. Таким образом, второе решение иррационально.
а значит, мы пришли к противоречию. Таким образом, второе решение иррационально.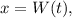 по определению дающая решение, т.е. являющаяся обратной, к функции
по определению дающая решение, т.е. являющаяся обратной, к функции  Функция вводится аналогично, скажем, функции
Функция вводится аналогично, скажем, функции 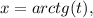 являющейся решением уравнения
являющейся решением уравнения  но в отличие от арктангенса, функция Ламберта используется намного реже в прикладных задачах (в основном в задачах теплопроводности), и поэтому – менее широко известна. Функция вводится на расширенной комплексной плоскости, т.е. алгебраически, а не арифметически, а значит по определению, может быть многозначной, и является таковой при отрицательных значениях аргумента
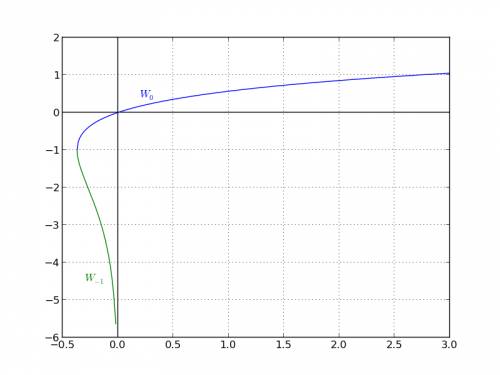
но в отличие от арктангенса, функция Ламберта используется намного реже в прикладных задачах (в основном в задачах теплопроводности), и поэтому – менее широко известна. Функция вводится на расширенной комплексной плоскости, т.е. алгебраически, а не арифметически, а значит по определению, может быть многозначной, и является таковой при отрицательных значениях аргумента 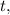 хотя нам достаточно будет знать лишь её действительные значения, которых при отрицательных аргументах всегда два. Вид действительных ветвей функции Ламберта представлен на приложенном изображении.
хотя нам достаточно будет знать лишь её действительные значения, которых при отрицательных аргументах всегда два. Вид действительных ветвей функции Ламберта представлен на приложенном изображении.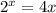 ;
;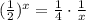 ;
; ;
;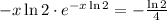 ;
;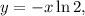 тогда:
тогда: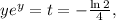 отсюда через функцию Ламберта:
отсюда через функцию Ламберта:
 ;
;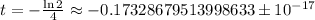 равна:
равна: ;
; искомое значение и вычисляя
искомое значение и вычисляя 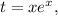 добиваясь его равенства
добиваясь его равенства 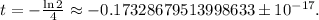
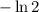 как раз и даст значение
как раз и даст значение  , что можно легко проверить подстановкой.
, что можно легко проверить подстановкой.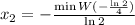 ;
;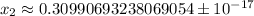 ;
;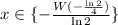 ;
; ;
;
Существует такая теорема Она гласит : Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его смежных сторон ,значит 2(3²+4²)=2*(9+16)=2*25=50. Значит сумма квадратов диагоналей параллелограмма равна 50 . Я предполагаю что этот параллелограм является прямоугольником. В прямоугольнике диагонали равны значит , квадрат одной диагонали равен 25 ,а просто диагональ 5 . Мы сможем найти площадь этого параллелограмма как сумма двух треугольников ,образованным любой диагональю. 2*общий корень p(p-a)(p-b)(p-d) ,Где p это полусумма (a+b+d)/2 ,A и b стороны параллелограмма,а D любая диагональ параллелограмма. (3+4+5)/2=12/2=6
2*на общий корень 6(6-3)(6-4)(6-5)= 6*3*2*1= 36 , это 6 в квадрате . 2*6=12.
Я понял что площадь параллелограмма зависит от угла и чем меньше угол между сторонами чем меньше его площадь .
Я писал долгий комментарий ,но он удалился ,короче я посчитал угол по площади параллелограмма ab*sin a,нашел третью сторону треугольника ,и по теореме косинусов она получилась 5.104 . Значит мои предложения то что диагональ равна пяти верны. P.S там угол будет 34⁰ мы разделили 2√11 на 12 и получили 0.55 ,а это sin 34 . Он не совсем прямоугольный ,потому что сторона больше пяти,а она уже не соответствует теореме Пифагора ,пифагоровый треугольник. А потом по теореме о сумме квадратов диагоналей параллелограмма ,находишь вторую диагональ. 5.104²+X²=2*(3²+4²) | 26.050+X =2*(9+16) =26.050 +X =2*25 | 26.050 +x= 50 . Отсюда X= 50-26.050=23.95. Не забываем что это квадрат другой диагонали . Найдем корень 23.95 это 4.89. Конечно если бы я был бы на огэ ,я бы нарисовал ,но сначала в теории попытался бы сделать синус какого то угла чтобы,с такими сторонами чтобы получилось 0.55 . По теореме Пифагора бы нашел третью сторону и транспортиром бы нашел угол. Есть конечно нахождения углов по подсчётам,но он сложный,и даже я не понимаю обратные тригонометрические функции,хоть и отличник в математике 8 класса
если p=0, то нет корней
если p не равно 0, то можно на него поделить
т.е. один корнень при любом p не равном нулю