ответ: 5
Пошаговое объяснение:
Пусть на некотором участке пути Кате осталось пробежать путь S, тогда по условию ее скорость в этот момент будет пропорциональна ближайшему целому числу, что не меньше чем S.
Например, если Кате осталось пробежать 7,3 км, то ее скорость пропорциональна числу 8. Аналогично, если ей осталось 7,8 км и тд. То есть, когда Катя пробежала 7 км, ее скорость становится пропорциональной 8 и остается такой (постоянной) пока она не пробежит еще один километр.
Аналогично, когда Катя бежит свой первый километр, ей осталось бежать от 14 до 15 километров, значит ее скорость пропорциональна 15, на втором километре она пропорциональна 14 и тд. На предпоследнем километре она пропорциональна 2, на последнем пропорциональна 1.
Пусть скорость Кати на последнем километре равна v, тогда сумма всех времен в часах на каждом километре выражается уравнением:
1/v + 1/(2v) + 1/(3v) +...+ 1/(15v) = 3 ч.
1+ 1/2 + 1/3 +...+ 1/15 = 3v
v = 1/3 * (1+ 1/2 + 1/3 +...+ 1/15)
Обозначим для удобства:
1+ 1/2 + 1/3 +...+ 1/15 = S
Откуда время проведенное на последнем километре:
t = 1/v = 3/S ч.
Переведем это время в минуты:
t = 60*3/s м.= 180/s м.
А наибольшее целое меньшее или равное одной десятой от числа минут равно, соответственно:
x = [t/10] = [18/s]
Где: [f] - целая часть числа f.
То есть нам необходим найти значение:
x = [18/(1+ 1/2 + 1/3 +...+ 1/15)]
Каких то вывести формулу n-го члена гармонического ряда не существует.
Существуют методы оценок снизу и сверху такого ряда, но к сожалению мощности неравенств в данном методе не хватит для решения поставленной задачи.
Подобрать наиближайшую геометрическую прогрессию и более простые ряды не удается.
Если кто-то все же придумает, то он молодец!
Остается только считать сумму этого ряда в лоб (всего 15 членов)
Если все аккуратно привести к общему знаменателю, то можно обнаружить, что сумма этого ряда:
3 < S < 3.6, примерно она равна 3.31.
Тогда верно неравенство:
18/3,6 <18/S < 18/3
5 <18/S < 6
x = [18/s] = 5
Добавление.
Придумал все же такой некий альтернативный вариант. Отбросим в каждой из дробей все разряды меньшие чем 0.01.
Максимальное отклонение от результата невелико и равно: 0,01 * 15 = 0,15
Произведем нужное нам сложение вынеся 0,01 за скобки:
0,01( 100+ 50 + 33 + 25 + 20 + 16 + 14 + 12 + 11 + 10 + 9 + 8 + 7 + 7 + 6) = 3,28
Тут уже складывать проще пареной репы, ну а найти например 1/13 и прочее до сотых легко, надо просто понять сколько полных цифр 13 умещается в 100, аналогично для 7 и тд. ( целочисленное деление 100 на 7, 11, 13 и тд).
Тогда с учетом сказанного выше:
3,28 <= S < 3,28 + 0,15 =3,43
А значит:
3 < S < 3,6
Вот такой вот .
Оба двухзначных числа оканчиваются на одну и ту же цифру (пересказал условие, хех). Произведение двух таких чисел может оканчиваться на 1, если они оканчиваются либо на 1, либо на 9.
Разложим число 2001 на множители. Сразу бросается в глаза, что оно делится на 3:
Разложим 667 на множители. Тут я считерю и воспользуюсь калькулятором, получается 23*29 — это простые числа. Я не знаю, как факторизовать их без калькулятора, кроме метода перебора.
То есть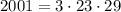 
. Есть два варианта сделать два двухзначных числа:
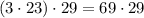— последние цифры одинаковы, подходит.
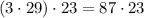— последние цифры одинаковы, не подходит.
ответ: 
.
P. S. Возможно, перейдя к десятичному представлению чисел и найдя там какие-то закономерности, можно решить проще без калькулятора. Попробуйте:
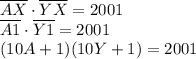
2)4290:5=858
3)2305*7=16135
4)858+16135=16993