Пусть х - это длина одной стороны, тогда длина второй стороны будет равна (8-х)
Пусть у - площадь этого прямоугольника,
тогда у=х(8-х)
Требуется найти значение х, при котором у принимает максимальное значение
у=-х*х+8х график этой функции - парабола, у которой ветви направлены вниз и пересекают ось абцисс в точках, т.е. у=0, х=0 ; у=0, х=8
Значит максимум находится в вершине этой параболы. Значит х=4, а следовательно
одна сторона этого прямоугольника равна 4, а вторая сторона 8-4=4, это квадрат.
ответ: каждая стороны этого прямоугольника равна 4 метрам.
Пошаговое объяснение:
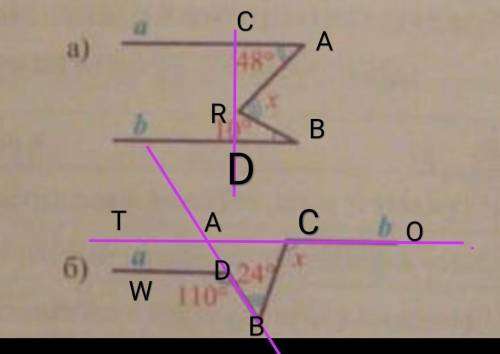
а) назовём точки А,В,R как на рисунке. проведём отрезок CD перпендикулярный прямой а и проходящий через точку R.
Рассмотрим полученный прямоугольный треугольник CRA с прямым углом С.
так как в прямоугольном треугольнике сумма острых углов равна 90°, то:
Угол CRA= 90°—угол CAR=90°–48°=42°.
Рассмотрим прямоугольный треугольник DRB с прямым углом D.
так как в прямоугольном треугольнике сумма острых углов равна 90°, то:
угол DRB=90°–угол RBD=90°–10°=80°
Угол ARB= 180°–угол CRA–угол DRB=180°–42°–80°=58°.
тоесть х=58°
ответ: 58.
б) продлим прямые а и b, назовём точки как показано на рисунке.
Так как прямые а и b по условию паралельны, то углы TAB и WDB являются соответственными при паралельных прямых а и b и секущей АВ, следовательно они равны и угол TAB=110.
Рассмотрим треугольник АВС.
угол ВАС смежный с углом ТАВ, следовательно он равен 180– угол ТАВ=180–110=70°.
Так как сумма всех углов треугольника равна 180°, то угол АСВ=180–угол АВС– угол ВАС= 180°–24°–70=86°.
Угол ВСО смежный с углом АСВ, следовательно: угол ВСО=180–угол АСВ=180–86=94°
тоесть х=94°
ответ: 94°
1) тогда диагональ квадрата равна стороне ромба ( свойства параллельных прямых пересеченных параллельными прямыми)
2) площадь квадрата равна половине квадрата его диагонали (свойства квадрата + т. Пифагора)
3) квадрат стороны ромба равен четверти суммы квадратов диагоналей (т. Пифагора+ свойства ромба)
4) итого: площадь квадрата вписанного в ромб равна восьмой части суммы квадратов диагоналей