Пусть количество батонов одного сорта равно Х. Тогда получаем уравнение
Х = (Х - 30) * 3
Х = 3 * Х - 90
2 * Х = 90
Х = 45
итак, одного сорта было 45 батонов, а всего батонов было 45 * 3 = 135
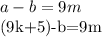

S=256 π см
Пошаговое объяснение:
Куля доторкаеця до всіх сторін правильного трикутника, медіана якого дорівнюе 12 см. Відстань від центра кулі до площини трикутника становить 4√3 см. Знайдіть площу поверхні кулі.
решение.
S=4πR², R=?
1. сечение шара плоскостью - круг. в круг вписан правильный треугольник с медианой 12 см. медианы, биссектрисы, высоты правильного треугольника в точке пересечения делятся в отношении 2:1 ,считая от вершины. точка пересечения медиан - центр описанной около треугольника окружности, => r=12:3. r=4 см, r - радиус описанной окружности
2. рассмотрим прямоугольный треугольник:
катет r =4 см - радиус секущей плоскости
катет h =4√3 см - расстояние от центра шара до секущей плоскости
гипотенуза R - радиус шара, найти по теореме Пифагора
R²=r²+h², R²=4²+(4√3)², R²=64
3. S=4*π*64, S=256 π
допустим, батонов одного сорта завезли х, тогда
(х-30)3=х
3х-х=90
х=90/2
х=45 батонов одного сорта
45*3=135 завезли всего