ертеден шығыс әлеміне танымал болған қала. Кейбір деректерге қарағанда осыдан екі жарым мың жыл бұрын оның орнында алғашқы қоныстар болған. ВІ – ВІІІ ғасырларда Отырар Сырдария өзенінің орта ағысындағы саяси орталық болды. Кейін ІХ – ХІІ ғғ. сол аймақтың басты қалаларының біріне айналады. Отырар Қазақ хандығы заманында мәдениеті мен экономикасы жақсы дамыған орталықтардың бірі болған. Отырар қаласының гүлденіп, орта ғасырдағы ірі қала орталығына айналуына оның орналасқан орны үлкен әсер етті. Бұл қаланың тез өсуіне қолайлы жағдай жасаған Ұлы Жібек жолы болды. В – ХВ ғғ Отырар қаласы Арал бойындағы көшпелі тайпалармен сауда жасайтын орталыққа айналды. Иран мен Орта Азиядан Сібірге, Монғолияға және Қытайға қатынайтын сауда жолындағы маңызды қала болды. Отырарға жан – жақтан көпестер келіп-кетіп жатты. Мұнда медреселер, базарлар, ұстаханалар, тіпті қонақүйлер мен мешіттер, монша, сауда дүкендері жұмыс істеген.
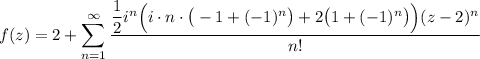
или проще
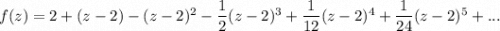
Пошаговое объяснение:
Вспомним формулу для разложения функции в ряд Тейлора
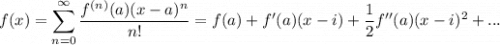
1 Запишем функцию
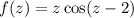
2 Найдем несколько производных:
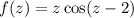
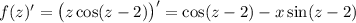
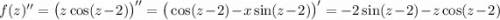
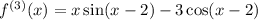
...
3 Найдем общий вид производной:
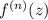
У нас в любом случае будет производная произведения, тогда наша производная распадется на какое-то количество слагаемых либо просто синуса, либо просто косинуса и слагаемое с х умноженным на либо синус, либо косинус.
Заметим, что производная синуса равна
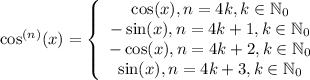
Тогда наше произведение в зависимости от n будет иметь разный вид.
Заметим, что всего различных слагаемых без множителя х будет n штук и все они будут иметь одинаковый знак
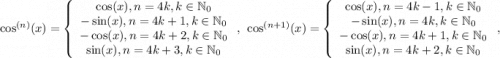 И по содержанию, и по знаку наши функции будут одинаковые. Осталось посчитать этот знак.
И по содержанию, и по знаку наши функции будут одинаковые. Осталось посчитать этот знак.
При n одинаковой четности знак один и тот же, в данной точке функция имеет вид
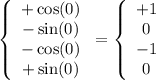
(производная 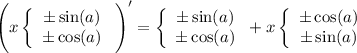 меняет местами функции)
меняет местами функции)
Мы можем записать для четных n знак у функции в виде 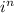 где i - мнимая единица, для нечетных n знак тоже можно записать в виде ее степени
где i - мнимая единица, для нечетных n знак тоже можно записать в виде ее степени 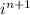
Для функции без множителя х формула такая (учитывая значения) 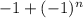 - мы должны будем еще умножить на степень для нечетных и также умножить на n (n раз брали производную)
- мы должны будем еще умножить на степень для нечетных и также умножить на n (n раз брали производную)
Для функции со множителем формула другая
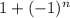
Чтобы избавится от ненужных двоек в первом случае, умножим все на  , и для того, чтобы все осталось как прежде во 2 случае, умножим только его часть на 2
, и для того, чтобы все осталось как прежде во 2 случае, умножим только его часть на 2
Тогда общая формула производной имеет вид
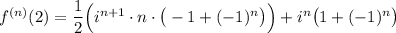
Можем вынести множитель 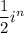 за скобки
за скобки
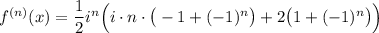
4 Тогда запишем ряд Тейлора
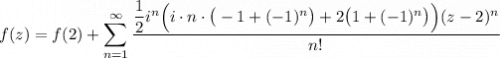
Начинаю с 1 так как писалась формула производной от 1.
f(2) = 2 * cos ( 2-2 ) = 2 * 1 = 2
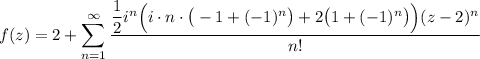
Это и есть ответ
2) f'(x)=-2/3*3x^2+2x=-2x^2+2x
3)f'(x)=(3/x+x^2)'(2-корень из x)-(3/x+x^2)(2-корень из x)'=
4) f'(x)=