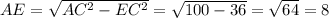Лодка плыла 1,4 ч по течению реки и 1,7 ч против течения.путь,который проплыла лодка по течению,оказалось на 2,2 км меньше пути,который она проплыла против течения.найдите скорость течения реки,если скорость лодки в стоячей воде 28 км/ч !

👇

Ответ:

alopavopa

16.02.2022

Пусть х км/ч - скорость течения реки. Собственная скорость лодки (скорость в стоячей воде) равна 28 км/ч, тогда по течению её скорость равна 28+х км/ч, а против течения 28-х км/ч.
Расстояние, которое лодка проплыла по течению реки, равно S(расстояние)=v(скорость)*t(время) = (28+х)*1,4 км, против течения (28-х)*1,7 км. Расстояние, которое лодка проплыла по течению на 2,2 км меньше.
Составим и решим уравнение:
1,7*(28-х) - 1,4*(28+х)=2,2
47,6-1,7х-39,2-1,4х=2,2
8,4-3,1х=2,2
-3,1х=2,2-8,4
-3,1х=-6,2
3,1х=6,2
х=6,2:3,1
х=2 км/ч - скорость течения реки.
ОТВЕТ: скорость течения реки равна 2 км/ч.

4,5(59 оценок)

Открыть все ответы

Ответ:

MIGSTERY10

16.02.2022

1)CB - ребро двугранного угла.
Чтобы найти линейный угол двугранного угла, необходимо построить плоскость ⊥ ребру BC.
Опустим AE ⊥ BC, DE ⊥ BC по теореме о трех перпендикулярах, где AE - проекция, DE - наклонная. BC - прямая проведенная через основание наклонной и перпендикулярная проекции.
AE и DE - находятся в одной плоскости и пересекаются, ВС - перпендикулярна AE и DE ⇒ перпендикулярна плоскости AED ⇒∠AED - линейный угол двугранного угла ∠ABCD.
2) ΔABC - равнобедренный, т.к. AB = AC = 10 см ⇒ опущенный перпендикуляр AE есть медиана ⇒ EC = DC/2 = 6 см.
3) ΔAEC - прямоугольный
По т. Пифагора
$AE = \sqrt{AC^{2} - EC^{2}} = \sqrt{100-36} = \sqrt{64} = 8$ (см)
4) т.к. AD = AE = 8(см) ⇒ ΔADE равнобедренный.
ΔADE - прямоугольный и равнобедренный ⇒ ∠AED = 45°
ответ: ∠AED = 45°

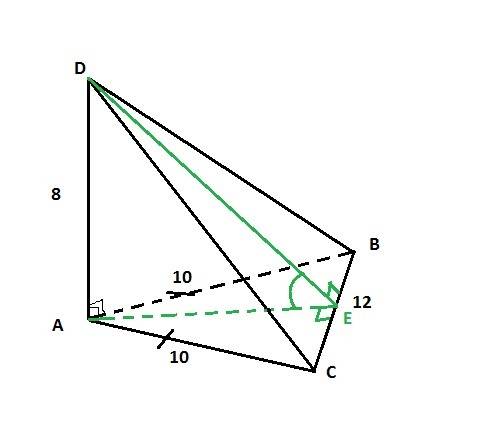
Втетраэдре авсд ребро ад перпендикулярно к плоскости авс ав=ас=10см вс=12 см ад=8 см найти линейный

Втетраэдре авсд ребро ад перпендикулярно к плоскости авс ав=ас=10см вс=12 см ад=8 см найти линейный

4,5(25 оценок)

Ответ:

vova147228

16.02.2022

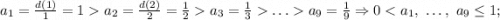
$a_1=\frac{d(1)}{1}=1 a_2=\frac{d(2)}{2}=\frac{1}{2}a_3=\frac{1}{3}\ldots a_9=\frac{1}{9}\Rightarrow 0$

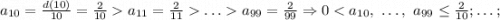
$a_{10}=\frac{d(10)}{10}=\frac{2}{10}a_{11}=\frac{2}{11}\ldots a_{99}=\frac{2}{99}\Rightarrow 0$

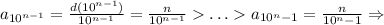
$a_{10^{n-1}}=\frac{d(10^{n-1})}{10^{n-1}}=\frac{n}{10^{n-1}}\ldots a_{10^n-1}=\frac{n}{10^n-1}\Rightarrow$

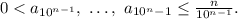
Последовательность 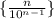$\{\frac{n}{10^{n-1}}\}$ стремится к нулю, поэтому исходная последовательность стремится к нулю по лемме о "двух правоохранителях" (милиционерах, полицейских, жандармах, копах и т.д - в зависимости от страны и эпохи).

Доказать, что 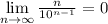$\lim\limits_{n\to \infty}\frac{n}{10^{n-1}}=0$ можно многими (с правила Лопиталя, теоремы Штольца, бинома Ньютона, неравенства Бернулли - кто подскажет еще ?).

Например, бином Ньютона дает нам следующую оценку:

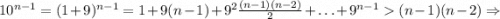
$10^{n-1}=(1+9)^{n-1}=1+9(n-1)+9^2\frac{(n-1)(n-2)}{2}+\ldots +9^{n-1}(n-1)(n-2)\Rightarrow$

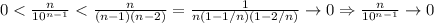Неравенство Бернулли применяем так:

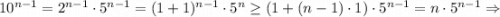
$10^{n-1}=2^{n-1}\cdot 5^{n-1}=(1+1)^{n-1}\cdot 5^n\ge (1+(n-1)\cdot 1)\cdot 5^{n-1}=n\cdot 5^{n-1}\Rightarrow$

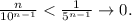
$\frac{n}{10^{n-1}}$

Лопиталь заменяет n на x, проверяет наличие неопределенности

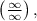$\left(\frac{\infty}{\infty}\right),$ вычисляет предел отношения производных:

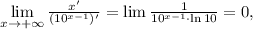$\lim\limits_{x\to+\infty}\frac{x'}{(10^{x-1})'}=\lim\frac{1}{10^{x-1}\cdot \ln 10}=0,$ и поскольку предел отношения производных существует и равен нулю, исходный предел также равен нулю.

Штольц не так хорошо известен, но наш предел вычисляет мгновенно. Однако я устал и (возможно) утомил читателя. Поэтому, памятуя Козьму Пруткова, заканчиваю.

4,7(23 оценок)

Это интересно:

Образование-и-коммуникации

19.12.2022

Методы высушивания цветов: вдохновляющие идеи и лучшие советы...

Кулинария-и-гостеприимство

03.02.2020

Как использовать вафельницу: подробный гид по приготовлению вафель...

Компьютеры-и-электроника

15.02.2021

Как избавиться от Mystart.Incredibar.Com: советы от экспертов...

Компьютеры-и-электроника