обозначаем: x-количество мужчину-количество женщинz-количество детейсоставляем уравнения: x+y+z=20 - всего пошло в поход20x+5y+3z=149 - это они неслиотталкиваясь от того что 1 ребенок несет 3 кг, получаем, что детей было либо 3, либо 13 (23 и более рассматривать нет смысла, ибо противоречит условию) - лишь в этих случаях получаем на конце числа килограммов цифру 9итак, у нас 2 случая: z=3 и z=13получаем совокупность двух систем: (система1)x+y+z=2020x+5y+3z=149z=3(система2)x+y+z=2020x+5y+3z=149z=3решения для этих систем будут такими : (система1)x=4y=13z=3(система2)x=5y=2z=13ответ: либо (4 мужчины, 13 женщин, 3 ребенка),
либо (5 мужчин, 2 женщины, 13 детей)
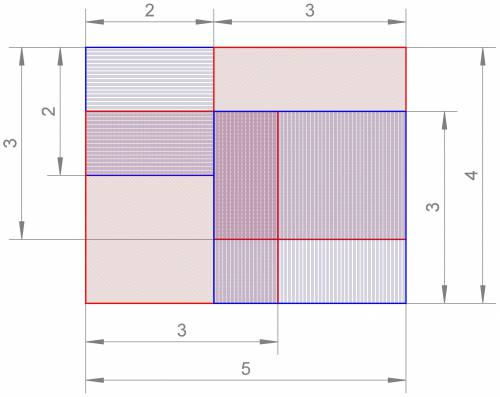
Возможно, тут без составления чертёжика будет трудно разобраться.
Смотрим на чертёж всего этого безобразия (на картинке внизу, сделано в масштабе, два ковра- синим, два ковра- красным), и видим, что есть следующие области перекрытия ковров:
1) по центру комнаты- прямоугольник 1 на 2 метра (там три слоя ковров)
2) слева- прямоугольник 2 на 1 метр (два слоя ковров)
3) снизу- квадрат 1 на 1 метр (два слоя ковров)
4) справа- квадрат 2 на 2 метра (два слоя ковров)
Всё, считаем площадь, которая накрыта коврами в 2 слоя:
Sдва_слоя = S₂ + S₃ + S₄ = 2*1 + 1*1 + 2*2 = 2 + 1 + 4 = 7 м²
На всякий случай: размеры областей считаются из размеров комнаты и ковров следующим образом:
2) по горизонтали= 2 м (равно размеру малого ковра)
по вертикали= (3 + 2) - 4 = 5 - 4 = 1 м (размеры ковров 3 и 2 метра (итого 5 м), их уложили вдоль стороны комнаты в 4 метра, значит перекрытие составляет 1 метр)
3) по горизонтали= (3 + 3) - 5 = 1 м
по вертикали= 4 - 3 = 1 м (левый ковёр размером в 3 метра, сторона комнаты в 5 метров, значит он не достаёт 2 метра до её правой стены)
4) по горизонтали= 5 - 3 - 2 м
по вертикали= (3 + 3) - 4 = 6 - 4 = 2 м
ответ: 304,2.