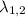logo
Вход Регистрация Спроси Mozg AI
М
Молодежь
К
Компьютеры-и-электроника
Д
Дом-и-сад
С
Стиль-и-уход-за-собой
П
Праздники-и-традиции
Т
Транспорт
П
Путешествия
С
Семейная-жизнь
Ф
Философия-и-религия
Б
Без категории
М
Мир-работы
Х
Хобби-и-рукоделие
И
Искусство-и-развлечения
В
Взаимоотношения
З
Здоровье
К
Кулинария-и-гостеприимство
Ф
Финансы-и-бизнес
П
Питомцы-и-животные
О
Образование
О
Образование-и-коммуникации
lol1039
lol1039
22.09.2022 18:43 •  Математика

54200-49*76-(24792+5874): (207-169)+705*108: 30 решите быстро

👇
Увидеть ответ
Ответ:
juliyamacko99
juliyamacko99
22.09.2022
54200-3724-(30666:38)+2538=54200-3724-807+2538=52207
4,4(5 оценок)
Ответ:
MonstorXXXX
MonstorXXXX
22.09.2022
54200-3724-807+2538=52207
52207 - ответ
4,4(100 оценок)
Открыть все ответы
Ответ:
кхммммм
кхммммм
22.09.2022
Мавзолей Карахана (мавзолей Аулие-ата) (каз. Қарахан кесенесі) — сооружён над могилой одного из представителей династии Караханидов. Памятник архитектуры XI века расположен в казахстанском городе Тараз в парке на пересечении улиц Толе би и Байзак батыра.
Считается, что мавзолей построен над могилой одного из представителей династии Караханидов — Шах-Махмуда Бугра Карахана. Мавзолей не сохранился до наших дней в первоначальном виде, в 1906 году он был перестроен и при сохранении конструкционного принципа утратил первоначальное архитектурно-декоративное убранство. Внутри мавзолея сохранилось ступенчатое надгробие. Строительство финансировал ишанТашкента Сайд Бакханов.
Впервые мавзолей был подробно исследован Борисом Денике и описан им в книге «Архитектурный орнамент Средней Азии». В 1982 году мавзолей Карахана был включен в список памятников истории и культуры Казахской ССР республиканского значения и взят под охрану государства. В советский период в мавзолее был размещен антирелигиозный музей.
В 2002 году была проведена реставрация мавзолея к 2000-летию города Тараза.
4,6(46 оценок)
Ответ:
кувшинкаВейВей
Решение в приложении.
Комментарии к решению:
Часть I
Решаю однородное уравнение для нахождения базис-векторов пространства решений уравнения. \lambda_{1,2} здесь - собственные числа, а

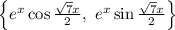\left\{e^x\cos\frac{\sqrt{7}x}{2},\ e^x\sin\frac{\sqrt{7}x}{2}\right\} - базис пространства решений уравнения.

Помним, что решение неоднородной системы есть функциональная комбинация векторов базиса:
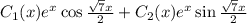C_1(x)e^x\cos\frac{\sqrt{7}x}{2}+C_2(x)e^x\sin\frac{\sqrt{7}x}{2}.

Часть III
Определяю матрицу Вронского (Вронскиан).
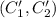Теперь нужно решить систему уравнений, где вектор-неизвестное (C'_1,C'_2) - это подходящие функции для функциональной комбинации.

Часть IV
Решение системы.
решения может быть любой, я использовал метод Крамера.

Часть V
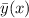Проинтегрировав функции (чего я не сделал), получаем множество решений уравнения \bar{y}(x) -  функциональную комбинацию (для нахождения решения, выполняющего начальные условия, нужно проинтегрировать 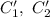C'_1,\ C'_2 и подставить начальные условия для нахождения свободного коэффициента получаемого при интеграции).

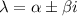P.S. метод попроще я, увы, не нашёл: все известные мне "хитрые подстановки" в частное решение, при комплексных лямбдах \lambda=\alpha\pm\beta i, ограничиваются 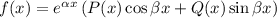f(x)=e^{\alpha x}\left(P(x)\cos\beta x+Q(x)\sin\beta x\right). Что подставлять для 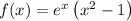f(x)=e^x\left(x^2-1\right) - без понятия.

Решить дифференциальное уравнение y-y'+2y=e^x(x^2-1)
4,5(70 оценок)
Это интересно:
О
Клюква стоит 250 рублей за кг, а малина 200....
О
Решить систему уравнений x2 + y2 + xy = 3...
О
Решить систему уравнений x2 + xy +y2 = 13...
О
В треугольнике АВС проведена биссектриса АК...
О
Водитель ехал с постоянной скоростью из города А в город Б...
О
Первые 300 км автомобиль ехал со скоростью 60 км/час...
О
В треугольнике АВС точка D на стороне АВ...
О
Из разных городов, расстояние между которыми 600 км...
О
Из пункта А в пункт B, расстояние между которыми 84 км...
Х
Правила и техника игры в карточную игру Скорость...
Новые ответы от MOGZ: Математика
Губанова1234
Что послужило основой для появления искусства? а) чувство прекрасного б) магия в) чувство совести...
Elka29677
Elka29677
02.08.2022
1) запиши две дроби, равные а) 1/2 б) 5/8 в) 15/60. 2) в равенстве вместо буквы запишите такое число, чтобы равенство было верным а) 10/25=2/с б) 2/3=а/33 в) 5/m=35/42....
aantip
aantip
02.08.2022
Сколько процентов составляет 3,8 м, 76 м,95 м от 475 м...
leralera799
leralera799
09.04.2020
Даны числа: 2/3, 1 2/9, 2 5/27, 35/81, 11/18. запишите каждое число в виде дроби со знаменателем : 1) 162b, 2) 324b, 3) 648b, где b - натуральное число...
mchervina
mchervina
09.04.2020
Вурне находится 7 белых и 5 черных шаров. найдите вероятность того что1)наудачу вынутый шар окажется черным...
анапияабдыганиева
Сколько будет если перевести 10м 15см в сантиметры?...
dron4ik226
dron4ik226
09.04.2020
Вгруппе 16 студентов.сколькими можно выбрать 4 из них для работы в летнем лагере...
даниил921
даниил921
09.04.2020
Как решить эту ? длина участка прямаугольной формы 70 метров а ширина на 30 метров .сколько шагов надо сделать чтоб пройти по его периметру? ( два шага состовляет 1...
typaya1911
typaya1911
09.04.2020
Вурне находиься 7 белых и 5 чёрных шаров . найдите вероятность того что 2) два наудачу вынутых шара окажутся черными...
usett
usett
09.04.2020
Для чего нужна рейсшина? как сней рработать?...

MOGZ ответил

Полный доступ к MOGZ
Живи умнее Безлимитный доступ к MOGZ Оформи подписку
О НАС
ПОМОЩЬ
App
.
.
logo
Вход Регистрация
Что ты хочешь узнать?
Спроси Mozg
Открыть лучший ответ