a) m + 1,8 = 18
m = 18 - 1,8 = 16,2
Проверка:
16,2 + 1,8 = 18
18 = 18
б) 10*p = 12,3
p = 12,3/10 = 1,23
Проверка:
10 * 1,23 = 12,3
12,3 = 12,3
в) a : 0,01 = 10
а = 10 * 0,01 = 0,1
Проверка:
0,1 : 0,01 = 10
10 = 10
г) 8,01 - y = 1,99
-у = 1,99 - 8,01
-у = -6,02
у = 6,02
Проверка:
8,01 - 6,02 = 1,99
1,99 = 1,99
е) 2,2 : z = 22
11/5 * 1/z = 22
11/5x = 22
11 = 110x
x = 0,1
Проверка:
2,2 : 0,1 = 22
22 = 22
Последний пример, возможно, можно решить намного легче, но от этого мой ответ не становится неверным. Если вы уже учите дроби - то можете спокойно воплощать его в действие.
Общее решение
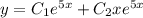
Частное решение
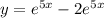
Пошаговое объяснение:
линейное однородное дифференциальное уравнение с заданными начальными условиями
y'' - 10y' + 25y = 0, y(0)=1,y'(0)=3
Запишем характеристическое уравнение k² - 10 ⋅ k + 25 = 0. Найдем его корни
k² - 10 ⋅ k + 25 = 0
k² - 2·5⋅ k + 5² = 0
(k - 5)² = 0
k₁ = k₂ = 5
Получили два совпадающих корня, следовательно, общее решение имеет вид
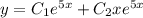
Для нахождения частного решения найдем производную функции
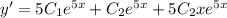
Подставляем начальные условия в функцию и ее производную
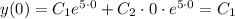
Из начальных условий у(0) =1
Следовательно С₁ = 1
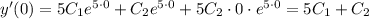
Из начальных условий y'(0)=3
Следовательно 5С₁ +С₂ = 3
С₂ = 3 - 5·1
С₂ = -2
Запишем частное решение уравнения
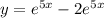
так как одна сторона нам известна, то нам известны все его стороны, потому что в квадрате все стороны равны.
Если сторона квадрата 33 км:
P = 33*4= 132 км
S = 33*33= 1089 км
Если сторона квадрата 270 дм:
P = 270*4= 1080 дм
S = 270*270=72900 дм