ответ:
левая часть:
1) определена на [0, 2a], a > = 0
2) становится четной функцией y после замены y = x - a, значит, если ваше уравнение имеет ровно один корень, то он равен a.
3) строго вогнута (пузиком вверх) как сумма функций, тем же свойством, следовательно, с учетом 2), строго возрастает [0, a] и строго убывает на [a, 2a]
отсюда ваше уравнение имеет единственный корень тогда и только тогда, когда a - корень уравнения. подставляем x = a в уравнение, получаем 2sqrt(a) = a, откуда a = 0 или a = 4. оба значения нам
пошаговое объяснение:
ps. и вот вам поиграть -
ответ: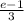
Пошаговое объяснение:
ответ: (e-1)/3
Пошаговое объяснение:
Найдём неопределённый интеграл функции e^(x^3)*x^2 чтобы использовать фундаментальную теорему исчисления.
.
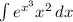Пусть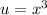 
, тогда ![x=\sqrt[3]{u}](/tpl/images/1117/3966/8c879.png)
.
![du = 3x^2dx \\ dx = \frac{du}{3x^2} = \frac{du}{3(\sqrt[3]{u} )^{2}} = \frac{du}{3u^{2/3}}](/tpl/images/1117/3966/82eee.png)
Делаем подстановку в наше изначальное выражение:
![\int{e^{x^{3}}x^2dx}=\int{e^{u}(\sqrt[3]{u})^{2}\frac{du}{3u^{2/3}} } = \int{ e^uu^{2/3}\frac{du}{3u^{2/3}} }](/tpl/images/1117/3966/640b8.png)
Здесь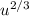 
сокращаются и мы имеем 
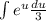. Выносим 
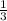за интеграл: 
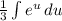. Теперь мы имеем знакомый интеграл, который равняется 
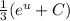, тоже самое что 
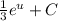. Подставляем 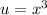и имеем 
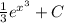. Используем фундаментальную теорему исчисления:
![\int\limits^1_0 {e^{x^3} x^2} = \frac{1}{3} e^{x^3}]_0^1=\frac{1}{3} e^{1^3}-\frac{1}{3} e^{0^3}=\frac{1}{3} e^1-\frac{1}{3} e^0=\frac{1}{3} e-\frac{1}{3}=\frac{e-1}{3}](/tpl/images/1117/3966/3089c.png)
f' (x)=2*1/2*1/sqr(x+5)=1/sqr(x+5)
f'(4)=1/sqr(4+5)=1/3, т.е. к=1/3