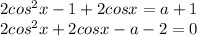
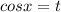
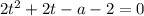
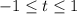
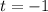 и
и 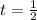 . Эти прямые проводим через данные точки, они выделены синим и красным. Почему это граничные точки? Пусть t заключено между этими прямыми. Если t = -1, то, как видно, всего одна точка общая с прямой t=-1 и окружностью(напомню, что прямая вида t = a - задаёт значение а косинуса угла на окружности). Тем более, если такие прямые лежат между синей и красной(эта область заштрихована синим). Здесь показана одна из таких прямых(зелёная). Как видим, она имеет с данным отрезком только одну точку пересечения, что нам и нужно. А вот прямая
. Эти прямые проводим через данные точки, они выделены синим и красным. Почему это граничные точки? Пусть t заключено между этими прямыми. Если t = -1, то, как видно, всего одна точка общая с прямой t=-1 и окружностью(напомню, что прямая вида t = a - задаёт значение а косинуса угла на окружности). Тем более, если такие прямые лежат между синей и красной(эта область заштрихована синим). Здесь показана одна из таких прямых(зелёная). Как видим, она имеет с данным отрезком только одну точку пересечения, что нам и нужно. А вот прямая 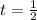 нам не подходит. В этой точке прямая пересекает наш отрезок дважды(в верхней полуокружности и в нижней). Значит, заведомо будет две серии решений, в каждой из которых по корню будут содержаться на этом отрезке(а нам нужен только один корень на отрезке). Соответственно, в правой области(она заштрихована красным), ТЕМ БОЛЕЕ это не выполняется. Помимо этого можно увидеть, что прямая t = 1 тоже нам подходит(ровно одна точка пересечения с окружностью).
нам не подходит. В этой точке прямая пересекает наш отрезок дважды(в верхней полуокружности и в нижней). Значит, заведомо будет две серии решений, в каждой из которых по корню будут содержаться на этом отрезке(а нам нужен только один корень на отрезке). Соответственно, в правой области(она заштрихована красным), ТЕМ БОЛЕЕ это не выполняется. Помимо этого можно увидеть, что прямая t = 1 тоже нам подходит(ровно одна точка пересечения с окружностью).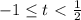 и
и 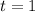 .
. 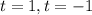 .
.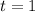 . Подставляя в квадратное уравнение, найдём отсюда соответствующее а:
. Подставляя в квадратное уравнение, найдём отсюда соответствующее а: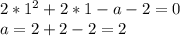
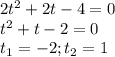
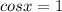 , устраивающее нас(его серия решений содержит единственный корень на отрезке) - a = 2 условию задачи удовлетворяет.
, устраивающее нас(его серия решений содержит единственный корень на отрезке) - a = 2 условию задачи удовлетворяет.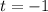
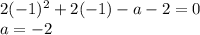
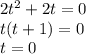 или
или 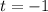
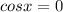 вновь имеет единственный корень на нашем отрезке(видно на круге). То есть, каждое t дало по одному корню на отрезке, в сумме - два корня для исходного уравнения. a = -2 нам абсолютно не подходит.
вновь имеет единственный корень на нашем отрезке(видно на круге). То есть, каждое t дало по одному корню на отрезке, в сумме - два корня для исходного уравнения. a = -2 нам абсолютно не подходит.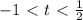 . Здесь надо быть поаккуратнее, поскольку необходимо отслеживать число корней квадратного уравнения и промежутки, в которых они находятся. Количество корней зависит от дискриминанта. Найдём его.
. Здесь надо быть поаккуратнее, поскольку необходимо отслеживать число корней квадратного уравнения и промежутки, в которых они находятся. Количество корней зависит от дискриминанта. Найдём его.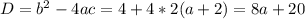
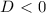 , то корней квадратное уравнение не имеет - на нет и суда нет.
, то корней квадратное уравнение не имеет - на нет и суда нет.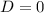 , то уравнение имеет один корень. Найдём его.
, то уравнение имеет один корень. Найдём его.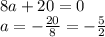
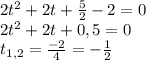 - такое значение t вписывается в наш промежуток для t, поэтому
- такое значение t вписывается в наш промежуток для t, поэтому 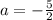 условию задачи удовлетворяет.
условию задачи удовлетворяет.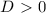 Самый сложный случай. Уравнение имеет два корня. Как же тогда получить в точности один корень на нужном отрезке? ответ прост: один корень должен вписываться в промежуток для t(там гарантированно будет одно решение на отрезке), а второй - не принадлежать ему(тогда гарантированно второй корень t не даст прибавку в подходящих x). Смотрите второй рисунок: либо меньший корень не принадлежит отрезку, либо больший.
Самый сложный случай. Уравнение имеет два корня. Как же тогда получить в точности один корень на нужном отрезке? ответ прост: один корень должен вписываться в промежуток для t(там гарантированно будет одно решение на отрезке), а второй - не принадлежать ему(тогда гарантированно второй корень t не даст прибавку в подходящих x). Смотрите второй рисунок: либо меньший корень не принадлежит отрезку, либо больший. 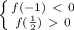 или
или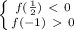
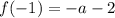
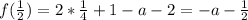
 ∈
∈ 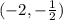
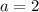 и
и 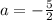 (не вошедшие сюда), записываем
(не вошедшие сюда), записываем ∈
∈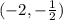 ,
, 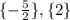
![Найдите все а при которых уравнение cos2x+2cosx=a+1 имеет только один корень на промежутке [-п/3; п]](/tpl/images/0775/9986/d2ff4.jpg)
![Найдите все а при которых уравнение cos2x+2cosx=a+1 имеет только один корень на промежутке [-п/3; п]](/tpl/images/0775/9986/6a7e4.jpg)
ответ:48 литров воды понадобится что-бы заполнить пол аквариума.