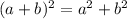 то это большое заблуждение!
то это большое заблуждение!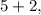 понятно, что
понятно, что 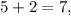 но мы не будем сразу возводить
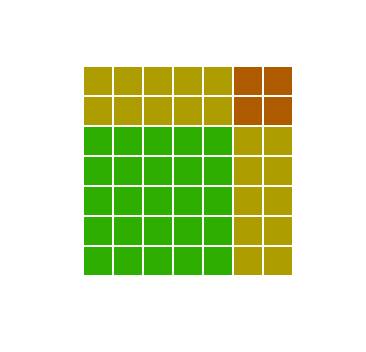
но мы не будем сразу возводить 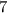 в квадрат, а попробуем разобраться в этом графически. Взглянем на рисунок (приложен к объяснению)
в квадрат, а попробуем разобраться в этом графически. Взглянем на рисунок (приложен к объяснению)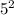 (это зелёный квадрат) и
(это зелёный квадрат) и 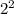 (это оранжевый квадрат), то мы не получим площадь квадрата со стороной
(это оранжевый квадрат), то мы не получим площадь квадрата со стороной 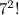 Чтобы получить правильную сумму
Чтобы получить правильную сумму 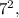 необходимо прибавить ещё два жёлтых прямоугольника с площадями
необходимо прибавить ещё два жёлтых прямоугольника с площадями 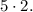
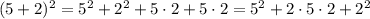 ;
;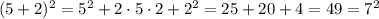 ;
;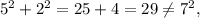 потому:
потому: 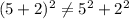 ;
;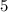 и
и 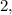 а для каких-то любых
а для каких-то любых  и
и 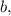 то получилось бы всё аналогично:
то получилось бы всё аналогично: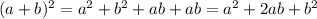 ;
; ;
;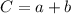 :
: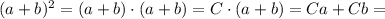
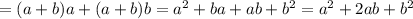 ;
;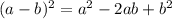 ;
;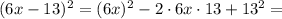
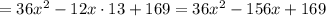 ;
;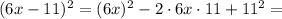
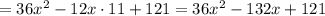 ;
;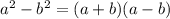 формула [2] ;
формула [2] ;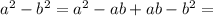
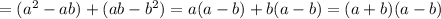 ;
;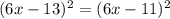 ;
;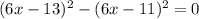 ;
;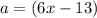 и
и 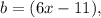 тогда:
тогда: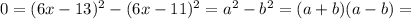
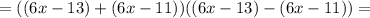
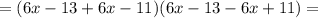
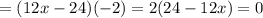 ;
;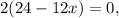 что возможно только если выражение в скобках равна нулю, т.е.:
что возможно только если выражение в скобках равна нулю, т.е.: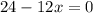 ;
;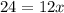 ;
;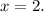
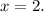
я помню что он нашел меня на улице больного мокрого и бес он забрал меня домой и вылечил меня я считаю что не только я но и все ребята 3его и оставшихся класов уважают его
P.S запятые расставь сам(а)