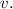Два банана и шесть яблок весят 1,4кг. четыре банана весят на 80г больше, чем пять яблок. сколько весит один банан и сколько одно яблоко?

👇

Ответ:

alexsey13

14.10.2020

Обозначим банан через b, яблоко через a. Составляем систему:
2b + 6a = 1,4
4b - 5a = 0,08

Умножаем первое уравнение на (-2) и складываем:
-4b - 12a = -2,8
4b - 5a = 0,08

-17a = -2,72
a = 0,16
b = (0,08 + 5a) / 4 = (0,08 + 5 * 0,16) / 4 = 0,22

ответ: банан весит 220 грамм, яблоко 160 грамм.

4,4(39 оценок)

Открыть все ответы

Ответ:

AnyaManankina

14.10.2020

Задачу можно решить методом «научного тыка»

Допустим, в какой-то момент малыш Федя обгоняет Соню на ходулях. Отметим это место специальной меткой, как условное начало круга. Как только он обгоняет Соню, он понимает, что (теперь уже) она – впереди него на расстоянии длины круговой дорожки (фактически она почти впритык позади него, но ведь дорожка круговая (!), а значит, Соня, как бы и впереди на расстоянии длины дорожки).

Пускай теперь до нового места встречи Соня пройдёт от метки какую-то часть круговой дорожки, назовём это «кусок дорожки», а малыш Федя до этого нового места встречи проедет на велосипеде целый круг и ещё такую же часть дорожки, т.е. такой же «кусок», как и Соня.

Новое место встречи, таким образом, сместилось от начальной метки на «кусок дорожки».

После второй встречи, Федя опять обгонит Соню и потом опять встретится с ней уже в третий раз со смещением ещё на один «кусок дорожки» от предыдущего места встречи, которое и так уже было смещено от начальной метки на «кусок дорожки», стало быть, третья встреча сместится от начальной метки на «два куска дорожки».

Второе место встречи сместилось от начальной метки
на «кусок дорожки», а Федя проехал лишний круг.

Третье место встречи сместилось от начальной метки
на «два куска дорожки», а Федя проехал два лишних круга.

Четвёртое место встречи сместится от начальной метки
на «три куска дорожки», а Федя проедет три лишних круга.

Пятое место встречи сместится от начальной метки
на «четыре куска дорожки», а Федя проедет четыре лишних круга.

Заметим, что если бы Соня к пятому месту встречи, смещённому от начальной метки на «четыре куска дорожки бы целый круг, то тогда Федя проехал бы 4 лишних круга и ещё «четыре куска дорожки», т.е. такое же расстояние, как и Соня, а значит ещё один добавочный круг.

И в таком случае, получилось бы, что Соня один круг, а Федя проехал пять кругов, что как раз и сходится с их соотношением скорости. Всё правильно, Федя ведь ездит в 5 раз быстрее, а значит, он и должен проехать в 5 раз больше, чем проходит Соня!

Значит, наше предположение верно. К пятой встрече Соня проходит полный круг, а стало быть, она приходит к начальной метке, которую мы отметили в месте первой встречи, т.е. место пятой встречи совпадает с местом первой встречи. Дальнейшие встречи станут совпадать со встречами в первом цикле рассуждений. Таким образом, всего существует 4 разных места, где Федя обгоняет Соню.

Так же, эту задачу можно решить и «аналитически», через введение неизвестного параметра скорости, и рассмотрения относительной скорости участников, т.е. скорости сближения.

Пусть скорость Сони равна v .

Тогда скорость Феди равна 5v .

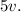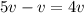Когда Федя догоняет Соню, их скорость сближения равна 5v - v = 4v

(вычитаем, поскольку Соня уходит от догоняющего её Феди, тем самым, как бы мешая ему себя догонять). Когда Федя в очередной раз обгоняет Соню, его удалённость от Сони, которую он встретит в будущем, в следующем месте обгона, составляет как раз один круг. За время, пока Федя доедет до нового обгона Сони, Соня пройдет по круговой дорожке в 4 раза меньшее расстояние, поскольку её скорость в 4 раза меньше скорости сближения. Из этого и следует, что за время между двумя очередными последовательными встречами, которые разделяют участников движения расстоянием в один круг, Соня проходит только четверть круговой дорожки. Значит за 4 дополнительные встречи (после первой начальной) она и пройдёт полный круг. Т.е. всего существует 4 места, в которых малыш Федя обгоняет Соню на ходулях.

О т в е т : (Б) в 4 точках.

4,6(63 оценок)

Ответ:

Maybejuliar1337

14.10.2020

Объем призмы ищется по такой формуле:

V = Sосн * h, где Sосн — площадь основания призмы, h — ее высота.

Так как все ребра призмы равны, то h = 6 см и в ее основании лежит равносторонний треугольник. Площадь равностороннего треугольника можно найти по следующей формуле:

S = a²√3 / 4, где a — сторона треугольника.

Воспользуемся ей и найдем площадь основания призмы, зная, что a = 6 см:

Sосн = 6²√3 / 4 = 9√3 см².

Теперь можно найти объем призмы:

V = 9√3 * 6 = 54√3 ≈ 93,5 см³.

ответ: объем прямой треугольной призмы равен примерно 93,5 см³.

Пошаговое объяснение:

4,6(8 оценок)

Это интересно:

Образование

06.01.2021

Клюква стоит 250 рублей за кг, а малина 200....