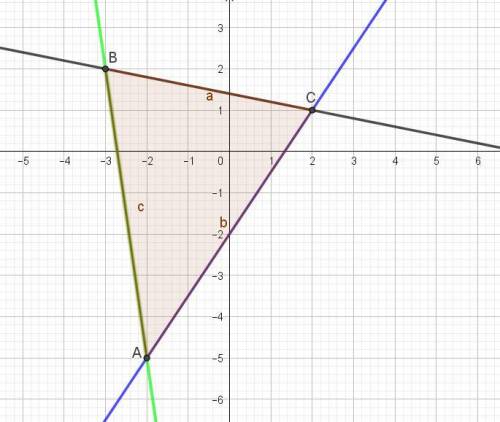
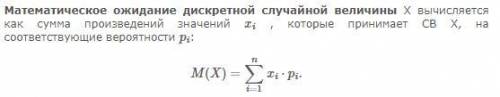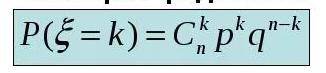Стороны треугольника лежат на прямых x+5у–7=0, 3x–2y–4=0, 7x+y+19=0. Вычислить его площадь S.
Находим координаты вершин треугольника как точки пересечения заданных прямых.
3x–2y–4=0, 3x–2y–4=0,
7x+y+19=0 |x2 = 14x+2y+38=0
17x + 34 = 0, x = -34/17 = -2.
y = (3/2)*x - (4/2) = y = (3/2)*(-2) - (4/2) = -3 - 2 = -5.
Точка А(-2; -5).
x+5у–7=0, |x-7 = -7x-35y+49=0
7x+y+19=0, 7x+y+19=0
-34y+68 = 0, y = -68/-34 = 2.
x = 7 - 5y = 7 - 5*2 = -3.
Точка В(-3; 2).
x+5у–7=0, |x(-3) = -3x-15y+21 = 0
3x–2y–4=0 3x–2y–4 = 0
-17y+17 = 0, y = -17/-17 = 1.
x = 7 - 5y = 7 - 5*1 = 2.
Точка С(2; 1).
Найдем вектора по координатам точек:
AB = {Bx - Ax; By - Ay; Bz - Az} = {-3 - (-2); 2 - (-5); 0 - 0} = {-1; 7; 0}
AC = {Cx - Ax; Cy - Ay; Cz - Az} = {2 - (-2); 1 - (-5); 0 - 0} = {4; 6; 0}
S = (1/2) |AB × AC|
Найдем векторное произведение векторов:
c = AB × AC
AB × AC =
i j k
ABx ABy ABz
ACx ACy ACz
=
i j k
-1 7 0
4 6 0
= i (7·0 - 0·6) - j ((-1)·0 - 0·4) + k ((-1)·6 - 7·4) =
= i (0 - 0) - j (0 - 0) + k (-6 - 28) = {0; 0; -34}
Найдем модуль вектора:
|c| = √(cx^2 + cy^2 + cz^2) = √(0^2 + 0^2 + (-34)^2) = √(0 + 0 + 1156) = √1156 = 34
Найдем площадь треугольника:
S = (1/2)* 34 = 17 .
5. M(Z) = 25,6
D(Z)= 112,8
6. а) M(X) = 2,64
б) D(X) = 0,32
Пошаговое объяснение:
5.
1) Для начала надо рассчитать Z и р-вероятность, т.е.:
Z=2X+4Y; р=р(х)*р(у).
1) Z1 = 2*(-5)+4*4 = 6 ; р=0,2*0,4=0,08
Z2 = 2*(-3)+4*4 = 10 ; р=0,1*0,4=0,04
Z3 = 2*1+4*4 = 18 ; р=0,1*0,4=0,04
Z4 = 2*3+4*4 = 22 ; р=0,6*0,4=0,24
Z5 = 2*(-5)+4*6 = 14 ; р=0,2*0,3=0,06
Z6 = 2*(-3)+4*6 = 18 ; р=0,1*0,3=0,03
Z7 = 2*1+4*6 = 26 ; р=0,1*0,3=0,03
Z8 = 2*3+4*6 = 30 ; р=0,6*0,3=0,18
Z9 = 2*(-5)+4*9 = 26 ; р=0,2*0,3=0,06
Z10 = 2*(-3)+4*9 = 30 ; р=0,1*0,3=0,03
Z11 = 2*1+4*9 = 38 ; р=0,1*0,3=0,03
Z12 = 2*3+4*9 = 42 ; р=0,6*0,3=0,18
2) теперь можно найти M(Z) - математическое ожидание (формула на рис. 1), т.е. это сумма всех Z*х
M(Z) = 6*0,08+10*0,04+18*0,04+22*0,24+14*0,06+18*0,03+26*0,03+30*0,18+26*0,06+30*0,03+38*0,03+42*0,18 = 25,6
3) дисперсия D(X) - это сумма всех Z^2*x - M(Z) (рисунок 2)
D(Z) = (6^2*0,08+10^2*0,04+18^2*0,04+22^2*0,24+14^2*0,06+18^2*0,03+26^2*0,03+30^2*0,18+26^2*0,06+30^2*0,03+38^2*0,03+42^2*0,18) - 25,6^2 = 112,8
6.
ПРОД1 = продукция с первого завода
ПРОД2 = продукция со второго завода
P(ПРОД1) = 3/7 = 0,4
P(ПРОД2) = 4/7 = 0,6
A = продукция (изделие) высшего качества
A|ПРОД1 = продукция высшего качества при условии, что продукция с первого завода
P(A|ПРОД1) = 0,85 (85%/100)
A|ПРОД2 = продукция высшего качества при условии, что продукция со второго завода
P(A|ПРОД2) = 0,9 (90%/100)
По формуле полной вероятности
P(A) = P(ПРОД1)*P(A|ПРОД1) + P(ПРОД2)*P(A|ПРОД2) = (0.4)*(0.85) + (0.6)*(0.9) = 0.34 + 0.54 = 0.88
Случайная величина X - число продукций высшего качества из 3 продукций. Данная случайная величина может принимать следующие значения: 0, 1, 2 и 3.
Событие {X=n} означает, что n продукций высшего качества и (3-n) продукций не высшего качества.
Случайная величина X имеет распределение Бернулли (рисунок 3) р - вероятность успеха
q - вероятность неудачи (не появления события)
n - количество появлений события
p = P(A) = 0.88
q = 1 - p = 1 - 0.88 = 0.12
Математическое ожидание
M(X) = np = 3*(0.88) = 2,64
Дисперсия
D(X) = npq = 3*(0.88)*(0.12) = 0,32