Сделать ! 1. выражение и затем найдите значение: а) а + 87 + 23, если а = 39 б) 147 + х- 47, если х = 87 в) у - 39 - 31, если у = 88. в таком виде: выражение= этого выражения если а= 39, то

👇

Увидеть ответ

Ответ:

АнастейшаГрей1

10.09.2020

а) Если а= 39, то а+87+23=39+110=149
б)Если х= 87то 147 + х- 47= 147+87-47=187
в) Если у=88, то у - 39 - 31=88-39-31=18

4,6(5 оценок)

Открыть все ответы

Ответ:

ivanova7nastya1

10.09.2020

Репродуктивная функция

Воспроизводство жизни, то есть рождение детей, продолжение человеческого рода. Забота о физическом и психическом здоровье подрастающего поколения.
Воспитательная функция

Формирование личности ребенка. Систематическое воспитательное воздействие семейного коллектива на каждого своего члена в течение всей его жизни. Постоянное влияние детей на родителей и других взрослых членов семьи. Семейное и общественное воспитание взаимосвязаны, дополняют друг друга и могут, в определённых границах, даже заменять друг друга, но в целом они неравнозначны и ни при каких условиях не могут стать таковыми. Семейное воспитание более эмоционально по своему характеру, чем любое другое воспитание, так как "проводником" его является родительская любовь к детям, вызывающая ответные чувства детей к родителям. Однако непорядок в воспитании может обернуться взаимной ненавистью, это тоже надо учитывать.
Обучающая функция

В семье происходит обучение подрастающего поколения. Здесь учат говорить, ходить, читать, считать и т.д. и т.п.
Коммуникативная функция

Посредничество семьи в контакте своих членов со средствами массовой информации, литературой и искусством. Влияние семьи на многообразные связи своих членов с окружающей природной средой и на характер ее восприятия. Организация внутрисемейного общения, досуга и отдыха, связанного с общением. Взаимное культурное и духовное обогащение.
Эмоциональная функция

Функция эмоционального удовлетворения. Отсутствие тепла и взаимопонимания, любви может быть причиной эмоциональных и поведенческих трудностей. Эмоциональная функция семьи - это удовлетворение ее членами потребностей в симпатии, уважении, признании, эмоциональной поддержке, психологической защите. Данная функция обеспечивает эмоциональную стабилизацию членов общества, активно содействует сохранению их психического здоровья.
Духовно-психотерапевтическая функция

Духовное общение — развитие личностей членов семьи, духовное взаимообогащение. Психотерапевтическая — позволяет членам семьи устраивать спонтанные психотерапевтические сеансы.
Развлекательно-рекреативная функция
Есть ещё защитная, функция социализации и другие

4,6(70 оценок)

Ответ:

анна2259

10.09.2020

Так как каждый пункт рассматривается в качестве отдельной задачи, замечательные точки треугольника всегда будут называться O.

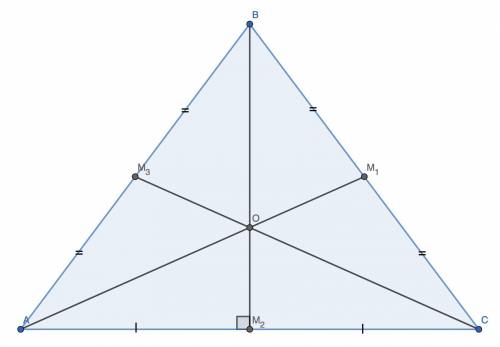
а) BM₂ точкой пересечения медиан делится в отношении BO : OM₂ = 2 : 1 ⇒ 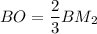$BO=\dfrac{2}{3}BM_2$ .

Так как AB = BC, BM₂ — высота. По теореме Пифагора 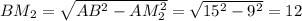$BM_2=\sqrt{AB^2-AM_2^2}=\sqrt{15^2-9^2}=12$ .

Тогда 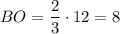$BO=\dfrac{2}{3}\cdot 12=8$

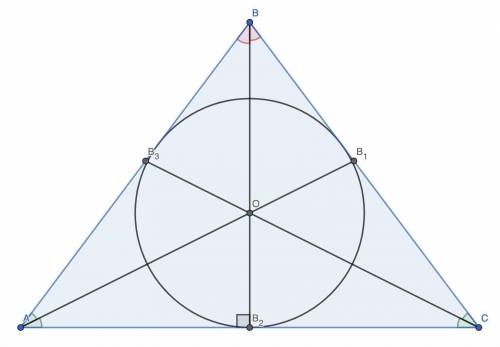
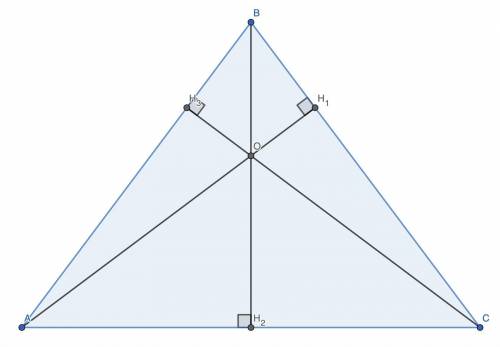
б) Точка пересечения биссектрис — центр вписанной окружности. Так как AB = BC, BB₂ — высота ⇒ OB₂ — радиус (r) вписанной окружности.

Площадь треугольника ABC

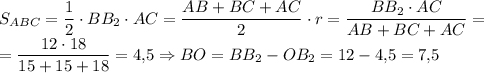
$S_{ABC}=\dfrac{1}{2}\cdot BB_2\cdot AC=\dfrac{AB+BC+AC}{2}\cdot r\Rightarrowr=\dfrac{BB_2\cdot AC}{AB+BC+AC}=\\=\dfrac{12\cdot 18}{15+15+18}=4{,}5\Rightarrow BO=BB_2-OB_2=12-4{,}5=7{,}5$

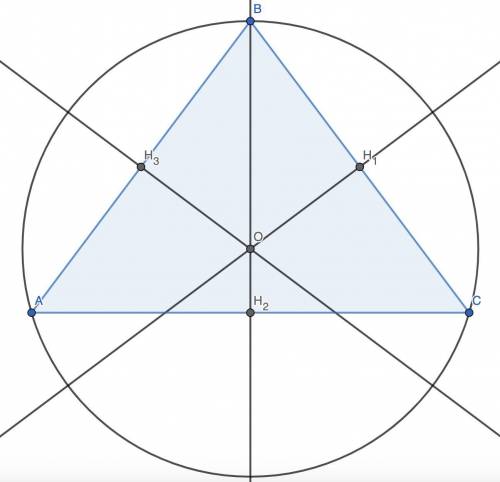
в) Точка пересечения серединных перпендикуляров — центр описанной окружности ⇒ OB — радиус (R) описанной окружности. Площадь треугольника ABC

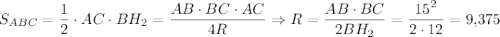
$S_{ABC}=\dfrac{1}{2}\cdot AC\cdot BH_2=\dfrac{AB\cdot BC\cdot AC}{4R}\Rightarrow R=\dfrac{AB\cdot BC}{2BH_2}=\dfrac{15^2}{2\cdot 12}=9{,}375$

г) Площадь треугольника ABC

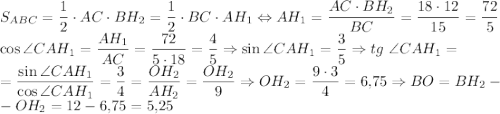
$S_{ABC}=\dfrac{1}{2}\cdot AC\cdot BH_2=\dfrac{1}{2}\cdot BC\cdot AH_1\Leftrightarrow AH_1=\dfrac{AC\cdot BH_2}{BC}=\dfrac{18\cdot 12}{15}=\dfrac{72}{5}\\\cos{\angle{CAH_1}}=\dfrac{AH_1}{AC}=\dfrac{72}{5\cdot 18}=\dfrac{4}{5}\Rightarrow \sin{\angle{CAH_1}}=\dfrac{3}{5}\Rightarrow tg~\angle{CAH_1}=\\=\dfrac{\sin{\angle{CAH_1}}}{\cos{\angle{CAH_1}}}=\dfrac{3}{4}=\dfrac{OH_2}{AH_2}=\dfrac{OH_2}{9}\Rightarrow OH_2=\dfrac{9\cdot 3}{4}=6{,}75\Rightarrow BO=BH_2-\\-OH_2=12-6{,}75=5{,}25$