Если конфеты в наборе не будут повторяться
Дети могут взять по две конфеты :
1) кс, ск - карамель, суфле
2) ки, ик - карамель, ирис
3) кт, тк - карамель, трюфели
4) си, ис - суфле, ирис
5) ст, тс - суфле, трюфели
6) ит, ти - ирис, трюфели
Чтобы наборы отличались, только 6 детей могут взять по 2 конфеты.
Решение по формуле сочетаний из 4 типов конфет по 2 штуки без повторений :

ответ : 6 детей
=====================================
Если конфеты в наборах могут повторяться, добавится ещё 4 варианта
Дети могут взять по две конфеты :
1) кс, ск - карамель, суфле
2) ки, ик - карамель, ирис
3) кт, тк - карамель, трюфели
4) си, ис - суфле, ирис
5) ст, тс - суфле, трюфели
6) ит, ти - ирис, трюфели
7) кк - карамель, карамель
8) сс - суфле, суфле
9) ии - ирис, ирис
10) тт - трюфели, трюфели
10 детей могут взять по 2 конфеты.
Решение по формуле сочетаний из 4 типов конфет по 2 штуки с повторениями :
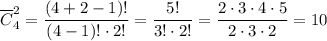
ответ : 10 детей
Если конфеты в наборе не будут повторяться
Дети могут взять по две конфеты :
1) кс, ск - карамель, суфле
2) ки, ик - карамель, ирис
3) кт, тк - карамель, трюфели
4) си, ис - суфле, ирис
5) ст, тс - суфле, трюфели
6) ит, ти - ирис, трюфели
Чтобы наборы отличались, только 6 детей могут взять по 2 конфеты.
Решение по формуле сочетаний из 4 типов конфет по 2 штуки без повторений :

ответ : 6 детей
=====================================
Если конфеты в наборах могут повторяться, добавится ещё 4 варианта
Дети могут взять по две конфеты :
1) кс, ск - карамель, суфле
2) ки, ик - карамель, ирис
3) кт, тк - карамель, трюфели
4) си, ис - суфле, ирис
5) ст, тс - суфле, трюфели
6) ит, ти - ирис, трюфели
7) кк - карамель, карамель
8) сс - суфле, суфле
9) ии - ирис, ирис
10) тт - трюфели, трюфели
10 детей могут взять по 2 конфеты.
Решение по формуле сочетаний из 4 типов конфет по 2 штуки с повторениями :
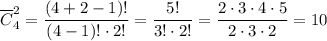
ответ : 10 детей
1я буква: вероятность, что выпадет правильная, составляет 2/5 (т.к. всего карточек пять, и из них две- с буквой Б)
если первая буква выпала правильная, то:
2я буква: карточек осталось четыре (Б,Е,Н,У), из них только одна- нужная (т.е. вероятность равна 1/4)
3я буква: карточек осталось три (Б,Е,Н), из них только одна- нужная (т.е. вероятность равна 1/3)
4я буква: карточек осталось две (Е,Н), из них только одна- нужная (т.е. вероятность равна 1/2)
5я буква: осталась только одна карточка (Н), т.е. вероятность равна 1/1=1 (такую вероятность обычно пишут как 100%, но мы не будем пока выражать в процентах, иначе не получатся следующие вычисления)
далее- чтобы слово получилось, должны выпасть все карточки, и вероятность этого будет равна произведению вероятностей выпадения всех карточек:
значит, это слово будет получаться в одном случае из шестидесяти (преобразование в десятичную дробь и в проценты не обязательно, только если у вас так принято записывать)