15 груш.
Пошаговое объяснение:
Пусть количество груш в сетке - х.
По условию количество груш в сетке составляет  от их количества в ящике. Тогда количество груш в ящике можно посчитать следующим образом:
от их количества в ящике. Тогда количество груш в ящике можно посчитать следующим образом:  .
.
Запишем условие, когда груш будет поровну:
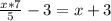
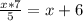
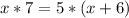
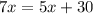
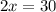
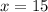
Проверка:
Если в сетке - 15 груш, то в ящике - 15 : 5 * 7 = 3 * 7 = 21 груша.
Если мы переложим 3 груши из ящика в сетку, то в ящике станет 18 и в сетке также станет 18, следовательно задача решена верно.
Если остались вопросы, задавайте в комментариях к моему ответу. С удовольствием . Я так понимаю, в условии были небольшие опечатки. Исправила, как понимаю
15 груш. Яблок - 0. Надеюсь в вопросе, записанном вами опечатка)
Пошаговое объяснение:
Пусть количество груш в корзине - х.
По условию количество груш в корзине составляет  от их количества в ящике. Тогда количество груш в ящике можно посчитать следующим образом:
от их количества в ящике. Тогда количество груш в ящике можно посчитать следующим образом:  .
.
Запишем условие, когда груш будет поровну:
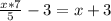
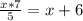
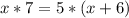
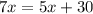
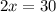
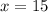
Проверка:
Если в корзине - 15 груш, то в ящике - 15 : 5 * 7 = 3 * 7 = 21 груша.
Если мы переложим 3 груши из ящика в корзину, то в ящике станет 18 и в корзине также станет 18, следовательно задача решена верно.
Если остались вопросы, задавайте в комментариях к моему ответу. С удовольствием
получить не менее одной шестерки при шести бросаниях 1- (5/6)⁶
(2) не получить ни одной шестерки при 12 бросаниях: (5/6)¹²
получить одну шестерку при 12 бросаниях: 12*(1/6)*(5/6)¹¹
получить не менее 2-х шестерок при 12 бросаниях: 1-(5/6)¹²- 12*(1/6)*(5/6)¹¹
(3) сравниваем (1) и (2) (берем разность и смотрим ее знак):
1- (5/6)⁶ -( 1-(5/6)¹²- 12*(1/6)*(5/6)¹¹)=
=(6¹² - 5⁶*6⁶-(6¹² - 5¹² - 12*5¹¹))/6¹²
берем только числитель и смотрим его знак:
(6¹² - 5⁶*6⁶-6¹² + 5¹² + 12*5¹¹) =
= - 5⁶*6⁶ + 5¹² + 12*5¹¹ = 5⁶*(5⁶ + 12*5⁵ - 6⁶)
берем величину в скобках:
17*5⁵-6⁶=17*25*125-216²=6469>0
таким образом, получить не менее одной шестерки при шести бросаниях более вероятно, чем получить не менее 2-х шестерок при 12 бросаниях