У нас есть три угла, величиной a° <= b° <= 4a°.
Причем сумма этих трех углов равна 360°.
a + b + 4a = 5a + b = 360
b = 360 - 5a
Решаем систему неравенств:
{ a <= 360 - 5a
{ 360 - 5a <= 4a
Приводим подобные
{ 6a <= 360
{ 9a >= 360
Получаем
{ a <= 60
{ a >= 40
Таким образом, наименьший угол а меняется от 40° до 60°, и получается
{ b >= 360 - 5a = 360 - 5*60 = 60; 4a = 4*60 = 240
{ b <= 360 - 5a = 360 - 5*40 = 160; 4a = 4*40 = 160
То есть размеры уголов меняются от (40; 160; 160) до (60; 60; 240)
Для угла а, который меняется от 40 до 60, всего есть 60 - 40 + 1 = 21 вариант.
Значит, и средний угол тоже может принимать 21 различное значение.
ответ: 21.
Примечание: если все три угла обязательно должны быть разными, то крайние варианты (40; 160; 160) и (60; 60; 240) отпадают, остается 19 вариантов.
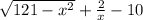
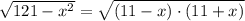
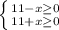
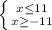
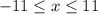
![x \in [-11, 0) \bigcup (0, 11]](/tpl/images/0795/3612/7c160.png)
x+y+z=26 (1)
x²+y²+z²=364 (2)
y²=x*z (3)
воспользуемся формулой (x+y+z)²=x²+y²+z²+2(xy+yz+xz)
26²=676=364+2(xy+yz+xz)⇒xy+yz+xz=(676-364)/2=156
учитывая (3) xy+yz+y²=y(x+y+z)=y*26=156 ⇒y=6
xz=6²=36
x+z=26-6=20 z=20-x
x(20-x)=36 ⇒ x²-20x+36=0
x1=18 x2=2 по т. Виета
у1=20-18=2 у2=20-2=18
ответ: 2, 6, 18 или 18, 6, 2