Sn=(2a1+d(n-1)*n/2
2Sn=(2a1+dn-d)n
2Sn=2a1n+dn²-dn
492=8n+3n²-3n
3n²+5n-492=0
n равен либо12, либо -41/3 (не подходит, т к меньше 0)
ответ:12
Пошаговое объяснение:
1) i ^ 13 = (i^2)^6 * i = (-1)^6 * i = i
i^100 = (i^2)^50 = (-1)^50 = 1
i^1993 = (i^100)^19 * i^93 = 1 * (i^2)^46 * i = i
2) (1 + i)^10
Воспользуемся формулой Муавра
z^n = r^n(cos φn + i*sin φn)
r - модуль, φ - аргумент комплексного числа
В нашем случае r = √2, φ = 
/4
(1 + i)^10 = (√2)^10 * (cos 10/4 + i*sin 10/4) = 32*(cos 5/2 + i*sin 5/2)=
= 32*(0+i*1) = 32i
Другой вариант решения:
(1 + i)^10 = ( (1 + i)^2 )^5 = (1 - 2i + i^2)^5 = (1 + 2i - 1)^5 = (2i)^5 = 32i * i^4 = 32i
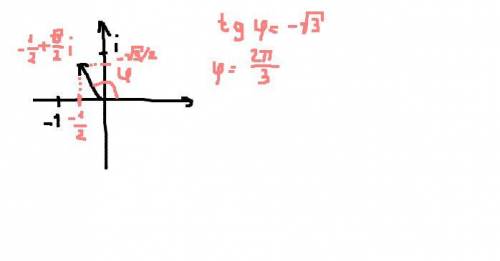
3) a = -1/2 + √3/2 * i
z^n = r^n(cos φn + i*sin φn)
Посчитаем модуль комплексного числа a:
r =√( (-1/2)^2 + (√3/2)^2) = 1
Аргумент φ = 2/3
a^4 = 1^4 * (cos 8/3 + i*sin 8/3) = -1/2 + i*√3/2 = a
a^11 = 1^11 * (cos 22/3 + i*sin 22/3) = -1/2 - i*√3/2
a^1992 = (a^4)^498 = a^498 =
= 1^498 * (cos 498*2/3 + i*sin 498*2/3) = cos 332 + i*sin 332 =
= 1
4) ( (1 + i)/(1 - i) )^1998 = ( (1 + i)^2 / 1^2 - i^2 )^1998 = ((1 + i)^2 / 2)^1998 =
= ((1^2 + 2i + i^2)/2)^1998 = ((1 +2i - 1)/2)^1998 = i^1998 = (i^2)^999 =
= (-1)^999 = -1
Sn = ((2a₁+(n-1)*d)/2)*n.
Приведём к общему знаменателю и приведём подобные.
Получим квадратное уравнение dn² + (2a₁-d)*n -2Sn = 0.
Подставив заданные значения, получим:
3n² + 5n - 492 = 0.
Квадратное уравнение, решаем относительно n:
Ищем дискриминант:D=5^2-4*3*(-492)=25-4*3*(-492)=25-12*(-492)=25-(-12*492)=25-(-5904)=25+5904=5929;
Дискриминант больше 0, уравнение имеет 2 корня:
n₁=(√5929-5)/(2*3)=(77-5)/(2*3)=72/(2*3)=72/6 = 12;
n₂=(-√5929-5)/(2*3)=(-77-5)/(2*3)=-82/(2*3)=-82/6= -(41/3) ≈ -13.6666666666667. - это отрицательное значение отбрасываем.
ответ: n= 12.