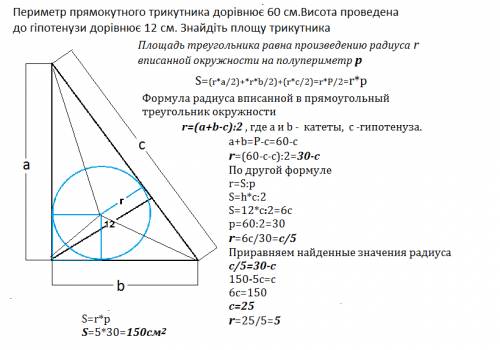
Периметр прямоугольного треугольника равен 60 см. Высота, проведенная к гипотенузе, равна 12 см. Найти площадь треугольника.
* * *
Площадь треугольника равна произведению радиуса r вписанной окружности на полупериметр р
Формула радиуса вписанной в прямоугольный треугольник окружности
r=(a+b-c):2 , где а и b - катеты, c -гипотенуза.
a+b=P-с=60-c
r=(60-c-c):2=30-c
По другой формуле
r=S:p
S=h*c:2
S=12*c:2=6c
р=60:2=30
r=6c/30=c/5
Приравняем найденные значения радиуса
c/5=30-c
150-5c=c
6c=150
c=25 см
r=25/5=5 см
S=r*p=5*30=150 см²
ответ:
пошаговое объяснение:
сначала построим график f(x)=2x+3.4
а теперь подумаем, что будет при взятии целой части числа.
вот, допустим, f(x)=1 без взятия целой части, при , тогда при любом , но при взятии целой части будет 1. далее, при некотором , f(x)=2.
но при любом
при идет прямая, в точка не выколота, а вот в где f(x)=1 выколота, а вот где f(x)=2 не выколота.
и так далее.
при f(x)< 0 все симметрично наоборот
на рисунке я постарался отметить все, что нужно. синяя прямая - исходная прямая графика y=2x+3.4, а вот черные кусочки - нужный график вместо с выколотыми точками.
пунктирами, по факту, отмечены разрывы функции. это перпендикуляры
Замена a - 5 = b, просто потому, что так проще писать.
x^2 - |x - b| = |x + b| - b^2
1) Пусть a < 5, тогда b = a - 5 < 0, -b > 0
а) Если x < b < 0 < -b, то |x - b| = b - x; |x + b| = -x - b
x^2 - b + x = -x - b - b^2
x^2 + 2x + b^2 = 0
Если уравнение имеет единственный корень, то D = 0
D/2 = 1 - b^2 = (1 + b)(1 - b) = 0
Так как по условию b < 0, то b = -1. a = b + 5 = 4
x = -1 - не подходит, потому что должно быть x < b.
б) Если b <= x < -b, то |x - b| = x - b; |x + b| = -x - b
x^2 - x + b = -x - b - b^2
x^2 = -b^2 - 2b = -b(b + 2)
При этом должно быть b < 0
Один корень x = 0 будет при b = -2, a = b + 5 = 3
a1 = 3
в) Если b < -b <= x, то |x - b| = x - b; |x + b| = x + b
x^2 - x + b = x + b - b^2
x^2 - 2x + b^2 = 0
Если уравнение имеет единственный корень, то D = 0
D/2 = 1 - b^2 = (1 + b)(1 - b) = 0
Так как по условию b < 0, то b = -1. a = b + 5 = 4
x = 1 = -b
a2 = 4
2) Пусть a = 5, тогда
x^2 - |x| = |x| - 0
x^2 = 2|x|
x1 = 0
x2 = 2
x3 = -2
Не подходит
3) Пусть a > 5, тогда b = a - 5 > 0, -b < 0
а) Если x < -b < 0 < b, то |x - b| = b - x; |x + b| = -x - b
x^2 - b + x = -x - b - b^2
x^2 + 2x + b^2 = 0
Если уравнение имеет единственный корень, то D = 0
D/2 = 1 - b^2 = (1 + b)(1 - b) = 0
Так как по условию b > 0, то b = 1. a = b + 5 = 6
x = -1 = -b - не подходит, потому что должно быть x < -b.
б) Если -b <= x < b, то |x - b| = b - x; |x + b| = x + b
x^2 - b + x = x + b - b^2
x^2 = -b^2 + 2b = -b(b - 2)
При этом должно быть b > 0
Один корень x = 0 будет при b = 2, a = b + 5 = 7
a3 = 7
в) Если -b < b <= x, то |x - b| = x - b; |x + b| = x + b
x^2 - x + b = x + b - b^2
x^2 - 2x + b^2 = 0
Если уравнение имеет единственный корень, то D = 0
D/2 = 1 - b^2 = (1 + b)(1 - b) = 0
Так как по условию b > 0, то b = 1. a = b + 5 = 6
x = 1 = b
a4 = 6
ответ: 3, 4, 6, 7