Пошаговое объяснение:
1) y = g(x):
Область определения: [-2; 6]
Область значения: [-3; 2]
Нули при x ∈ {2, 6}
На [-2; 0) ∪ (4; 6] монотонно убывает.
На (0; 4) монотонно возрастает.
На [-2; 2) отрицательна.
На (2; 6) положительна.
В (0; -3) absmin.
В (4; 2) absmax.
2) y = f(x):
Область определения: [-5; 4]
Область значения: [-2; 4]
Нули при x ∈ {-3.5, 1, 3}
На (-1; 2) монотонно убывает.
На [-5; -1) ∪ (2; 4] монотонно возрастает.
На [-5; -3.5) ∪ (1; 3) отрицательна.
На (-3.5; 1) ∪ (3; 4] положительна.
В (2; -1.5) locmin.
В (-1; 4) absmax.
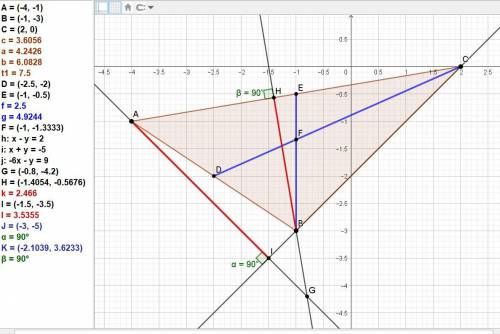
Даны координаты вершин A(-4;-1) B(-1;-3) C(2;0).
Найти точки пересечения медиан и высот треугольника АВС.
1) Точка F пересечения медиан треугольника имеет следующие координаты:
x(F) = (x1+x2+x3)/3, y(F) = (y1+y2+y3)/3,
где A(x1,y1), B(x2,y2) и C(x3,y3) − вершины треугольника ABC.
Подставим координаты точек и получаем ответ.
х(F) = (-4+(-1)+2)/3 = -1,
у(F) = (-1+(-3)+0)/3 = -4/3.
ответ: точка пересечения медиан F(-1; (-4/3)).
2) Находим уравнения сторон, для чего определяем векторы АС и ВС.
Вектор АС = ((2-(-4)); (0-(-1)) = (6; 1).
Уравнение АС: (x + 4)/6 = (y + 1)/1 каноническое.
x – 6y – 2 = 0 общее.
Вектор ВС = ((2-(-1)); (0-(-3)) = (3; 3).
Уравнение ВС: (x + 1)/ 6 = (y + 3)3 каноническое.
3x – 6y – 15 = 0 общее или, сократив на 3
x – 2y –5 = 0.
Теперь находим уравнения высот к этим сторонам.
Уравнение высоты BH.
Она перпендикулярна стороне AС.
Вектор AС найден и равен (6; 1).
Для прямой BH он будет нормальным вектором.
Составляем уравнение прямой по точке В(-1; -3) и нормальному вектору (6; 1).
Уравнение BH: 6*(x + 1) + 1*(y + 3) = 0,
6x + 6 + y + 3= 0,
6x + y + 9 = 0.
Уравнение высоты AI.
Она перпендикулярна стороне BС.
Вектор BС найден и равен (3; 3).
Для прямой AI он будет нормальным вектором.
Составляем уравнение прямой по точке A(-4; -1) и нормальному вектору (3; 3).
Уравнение AI: 3*(x + 4) + 3*(y + 1) = 0,
3x + 12 + 3y + 3= 0,
3x + 3y + 15 = 0 или, сократив на 3:
x + y + 5 = 0.
Координаты точки G пересечения высот найдём, решив систему:
{6x + y + 9 = 0
{ x + y + 5 = 0 вычтем из первого уравнения второе.
5x + 4 = 0, отсюда х = -4/5 = -0,8.
у = -х – 5 = -(-0,8) – 5 = -4,2.
ответ: точка пересечения высот G(-0,8; -4,2).
2. 9485 * 9 - (9485 - 9) = 85365 - 9476 = 75889.