Пропорциональность — это взаимосвязь между двумя величинами, при которой изменение одной из них влечет за собой изменение другой во столько же раз.
Пропорциональность бывает прямой и обратной. В данном уроке мы рассмотрим каждую из них.
Содержание урока
Прямая пропорциональность
Обратная пропорциональность
Прямая пропорциональность
Предположим, что автомобиль двигается со скоростью 50 км/ч. Мы помним, что скорость это расстояние, пройденное за единицу времени (1 час, 1 минуту или 1 секунду). В нашем примере автомобиль двигается со скоростью 50 км/ч, то есть за один час он будет проезжать расстояние, равное пятидесяти километрам.
Изобразим на рисунке расстояние, пройденное автомобилем за 1 час
Если мы ищем производную по х то ответ будет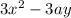 
Если мы ищем производную по у то ответ будет 
Если мы берём производную по а то ответ будет просто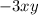 
Так же производную невозможно искать если приравнивать к нулю.
Рассчитывал производную по основной формуле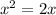 
. Если мы берём производную от степени то уменьшаем её на 1 и выносим изначальное число степени перед иксом.
А так же если у мы берём допустим по х то там где просто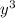 
то это равно 0 и мы не учитываем, а если есть х и у то смотрим на степень х и у и действуем по схеме выше. Так как у нас в конце стоит 3ху и х и у в первой степени, то мы просто убираем либо х либо у, и оставляем либо х либо у.
Пошаговое объяснение:
Один проходит круг за t c, а второй за t+3 с.
Значит, скорости у них v1 = 1/t (км/с), v2 = 1/(t+3) (км/с).
Что значит фраза "Первый догоняет второго каждые 12 мин" ?
Это значит, что за 12 мин = 720 с 1-ый делает n кругов, а 2-ой (n-1).
{ T1 = n/v1 = nt = 720 c
{ T2 = (n-1)/v2 = (n-1)(t+3) = 720 c
Раскрываем скобки у приравниваем левые части
{ nt = nt - t + 3n - 3
{ n = 720/t
Упрощаем 1 уравнение и подставляем в него 2 уравнение
t + 3 = 3n = 3*720/t
t^2 + 3t - 2160 = 0
D = 9 - 4(-2160) = 9 + 8640 = 8649 = 93^2
t1 = (-3 - 93)/2 < 0
t2 = (-3 + 93)/2 = 90/2 = 45 c - это время 1-го велосипедиста на один круг.
t + 3 = 48 c - это время 2-го велосипедиста на один круг.