Условие:
I цех - 24 шк.
II цех - ?, на 6 шк. > чем I
Всего 6 грузовиков
1 гр.- ? шкафов
1) 24 + 6 = 30 (ш.) - изготовил второй шех
2) 24+30=54 (ш.) - изготовили оба цеха
3) 54 : 6 = 9 (ш.) - погрузили на один грузовик
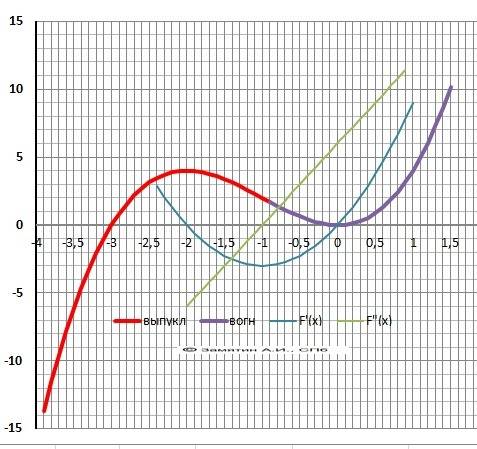
1.Область определения D(x) - Х∈(-∞;+∞) - непрерывная. Нет деления на ноль.
2. Пересечение с осью Х. Y=0 при х = 0 и х = -3. (ставим две точки на оси ОХ)
3. Пересечение с осью У. У(0) = 0. (ставим точку на оси ОУ)
4. Поведение на бесконечности.
limY(-∞) = - ∞ limY(+∞) = +∞ (слева вниз - справа вверх)
5. Исследование на чётность.
Y(-x) = -x³ +3x² ≠ Y(x).
Функция ни чётная ни нечётная.
6. Производная функции.Y'(x)= 3*x² + 6*x = 3*x*(x-2).
Корень при Х1=0 и Х2= 2
Схема знаков производной.
_ (-∞)__(>0)__(х1=0)___(<0)___(x2=2)__(<0)_____(+∞)__
Функция убывает МЕЖДУ корнями.
7. Локальные экстремумы.
Максимум Ymax(-2)= 4 , минимум – Ymin(0)=0.
8. Интервалы возрастания и убывания.
Возрастает - Х∈(-∞;-2)∪(0;+∞) , убывает = Х∈(-2;0).
8. Вторая производная - Y"(x) = 6*х+6 =6*(x+1)=0.
Корень производной - точка перегиба Y"(x)= 0. Х= -1
9. Выпуклая “горка» Х∈(-∞;-1), Вогнутая – «ложка» Х∈(-1;+∞).
10. Область значений Е(у) У∈(-∞;+∞)
11. График в приложении.
I цех - 24 ш.
II цех - ? ш., на 6 ш. >, (чем I (рисуешь стрелку от II к I)
I груз./а. - ? ш.
Всего - на 6 груз./а. (фигурная скобка)
1) 24+6=30 (ш.) - изготовил II цех.
2) 24+30=54 (ш.) - всего (изготовили оба цеха).
3) 54:6=9 (ш.) - погрузили на 1 грузовой автомобиль.
ответ: 9 книжных шкафов грузили на один грузовой автомобиль.