Изменение скорости автобуса можно представить в виде графика (смотрите ниже).
Тогда пройденный путь будет площадью прямоугольного треугольника (на чертеже выделен цветом), ограниченного в данном случае осью абсцисс, прямыми  (м/с) и
(м/с) и  (с).
(с).
Для того, чтобы узнать его площадь, можно взять интеграл, как рекомендуется в задании:

Но можно ограничиться формулой площади прямоугольного треугольника (половина произведения длин катетов). Один катет которого равен 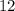 , а другой -
, а другой - 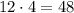 :
:
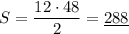
Но так или иначе, получаем, что автобусом будет пройдено  метров.
метров.

Второе решение. Пусть O – середина отрезка BD. Прямая BD перпендикулярна плоскости AOA1. Следовательно, плоскости BDA1 и AOA1 перпендикулярны. Искомым перпендикуляром, опущенным из точки A на плоскость BDA1, является высота AH прямоугольного треугольника AOA1, в котором AA1 = 1, AO = , OA1 =√6/2 . Треугольники AOA1 иHOA подобны по трем углам. Следовательно, AA1:OA1 = AH:AO. Откуда находим AH = √3/3.
Третье решение. Пусть O – середина отрезка BD. Прямая BD перпендикулярна плоскости AOA1. Следовательно, плоскости BDA1 и AOA1 перпендикулярны. Искомым перпендикуляром, опущенным из точки A на плоскость BDA1, является высота AH прямоугольного треугольника AOA1, в котором AA1 = 1, AO = , OA1 =√6/2 . Откуда sin угла AOA1=√6/3
и, следовательно, AH=AO* sin угла AOH=√3/3