для начала выполним действия в скобках. Сперва произведем деление, потом вычитание.
1)1 5/9 : 7/24, приведем дробь 1 5/9 в неправильную дробь, для этого (1*9+5)/9=14/9. Пользуясь правилом деления дробей , перевернем и умножаем ее на 24/7, 14/9* 24/7=(14*24)/(9*7) сократив и числитель и знаменатель на 7 и 3 получаем 16/3 =5 1/3
2)7-5 1/3 , 7 можно представить в виде 6 +3/3,тогда получится 6-5+(3/3-1/3)= 1 2/3 прежде чем делить на 1 7/20 переведем ее в неправильную дробь (1*3+2)/3=5/3, 1 7/20=27/20, применив правило деления дробей 5/3 * на перевернутую дробь 20/27
4)5/3* 20/27=100/81 или 1 целая 19/81
ответ 1 целая 19/81
Пошаговое объяснение:
1) с первым интегралом все достаточно просто
здесь мы перейдем к повторным интегралам и получим вот что
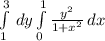
сначала вычисляем внутренний интеграл
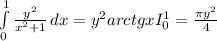
теперь вычисляем внешний интеграл
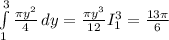
это и есть ответ 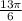
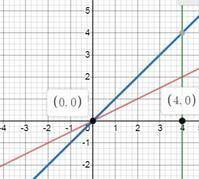
2) со вторым придется построить графики, чтобы определить границы интегрирования по х
тут мы видим, что х изменяется 0≤х≤4
в общем-то нижний предел интегрирования можно было бы найти и путем выяснения, в какой точке пересекаются графики (через уравнение х/2 = х корень данного уравнения х=0), но лучше все же строить график
теперь, собственно приступаем к переходу и интеграции
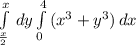
внутренний интеграл
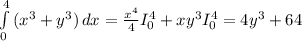
внешний интеграл
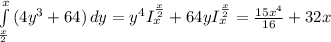
ответ 
1) 27,5 + 1,3 = 28,8 (км)
2)28,8 : 1,2 = 24(км)
3) 27,5 + 24 + 28,8 = 80,3(км)
ответ: 80,3 км