Любой объект (изделие, машина или система) обладает характерными свойствами. Некоторые из этих свойств полезны, но другие бывают более или менее нежелательными. Наиболее важное свойство из всех - ϶ᴛᴏ основная функция изделия, потому что она потребителю в удовлетворении его нужд. Другими желательными свойствами бывают приятный внешний вид, легкость перемещения, безопасность, долговечность и надежность. Прежде чем приступить к конструированию, конструктор должен , должна быть в сотрудничестве с потребителем, составить перечень желаемых свойств изделия. В процессе конструирования, когда изделие создается, именно эти свойства определяют выбор принимаемых конструктивных решений.
К сожалению, нельзя конструировать изделия таким путем, чтобы желаемые свойства определялись одно за другим, так как эти свойства являются независимыми переменными. При этом принято считать, что среди всех можно выделить пять базовых свойств, которые в сумме полностью определяют изделие. В целом таким свойством для изделия является структура (ᴛ.ᴇ. элементы изделия и их взаимосвязь), а для каждого элемента – форма, материал, размеры, поверхность. Важно подчеркнуть, что эти свойства являются переменными, которыми конструктор может манипулировать, а изделие создается последовательными решениями вопросов, связанных с этими переменными. Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, все другие свойства, как полезные, так и нежелательные, выводятся из этих базовых свойств. При этом, поскольку эта цель не всегда достигается, крайне важно различать желаемые свойства и фактически полученные свойства, приходя, таким образом к следующей модели процесса конструирования
-10
Пошаговое объяснение:
Нам тут понадобится правило Лопиталя.
если 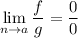 или
или 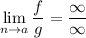 то
то 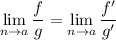
1
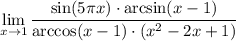
2 Вынесем -1 по формуле 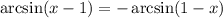
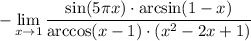
3 Запишем предел произведения дробей как произведение пределов
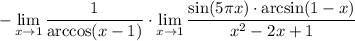
4 Подставим в первом пределе значение и посчитаем
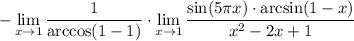
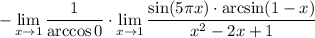
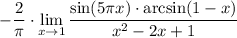
5 Cоберем квадрат в знаменателе 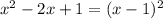
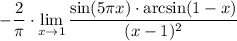
6 Получили предел вида  воспользуемся правилом Лопиталя
воспользуемся правилом Лопиталя
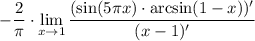
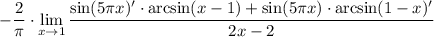
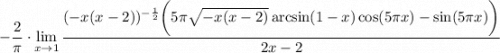
Тут я сразу вынес за скобки
7 Вынесем  (взял 2 в знаменателе) за предел и сократим
(взял 2 в знаменателе) за предел и сократим
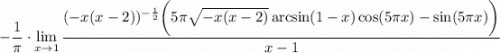
8 Распишем как произведение пределов
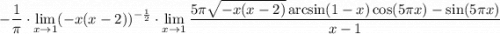
9 Посчитаем первый предел
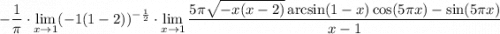
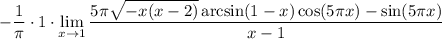
10 Распишем разность дробей в пределе
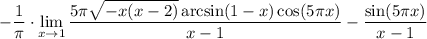
11 Распишем предел разности как разность пределов
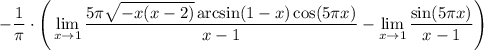
12 Распишем первый предел как произведение пределов и вынесем 5π
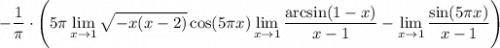
13 Посчитаем первый предел
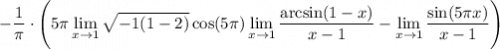
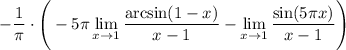
14 В первом пределе снова неопределённость  , снова Лопиталем
, снова Лопиталем
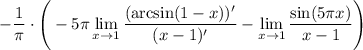
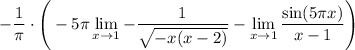
15 Теперь мы можем посчитать первый предел
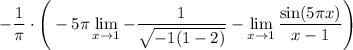
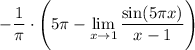
16 Снова используем правило Лопиталя, так как у нас неопределённость 
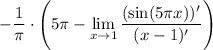
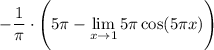
17 Выносим константу
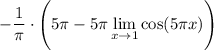
18 Посчитаем предел
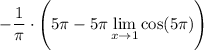
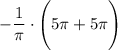
19 Досчитываем!
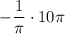

МЫ ПОЛУЧИЛИ ОТВЕТ
36
25
180
72
900
25
32
50
75
800
28
25
140
56
700