Пошаговое объяснение:
Произведение равно нулю, когда один из множителей равен нулю
а)18⋅(x-24)=0 → х - 24 = 0 → х = 24
б)(18+х)⋅32=0 → 18 + х = 0 → х = - 18
в)(36-х)⋅(х+11)=0
1) 36 - х = 0 → х = 36;
2) х + 11 = 0 → х = - 11
ответ: х = 36; - 11
г)2⋅х⋅(712-х)=0
1) х = 0
2) 712 - х = 0 → х = 712
ответ: х = 0; 712
д)(4⋅х-16)⋅65=0 → 4х - 16 =0 → 4х = 16 → х = 4
е)(2-2⋅х)⋅(х+11)=0
1) х + 11 = 0 → х = -11;
2) 2 - 2х = 0
2х = 2 → х = 1
ответ: х = - 11; 1
Докажем, что сумма этих чисел делится на медиану слагаемых (с показателем степени 1). Для p = 1 это очевидно, но 1 - число не составное. Докажем, что в остальных случаях сумма чисел k^p и (2m - k)^p делится на m (где m - медиана со степенью 1).
k ≡ k (mod m)
2m - k ≡ (-k) (mod m)
k^p + (-k)^p ≡ 0 (mod m) (для нечётного p)
Собрав все числа (кроме медианы) в такие группы получаем, что сумма чисел в каждой из них делится на m. Это означает, что вся сумма делится на m. Так как m меньше m^p, то вся сумма больше m, следовательно, имеет не меньше трёх делителей, что означает, что число составное.
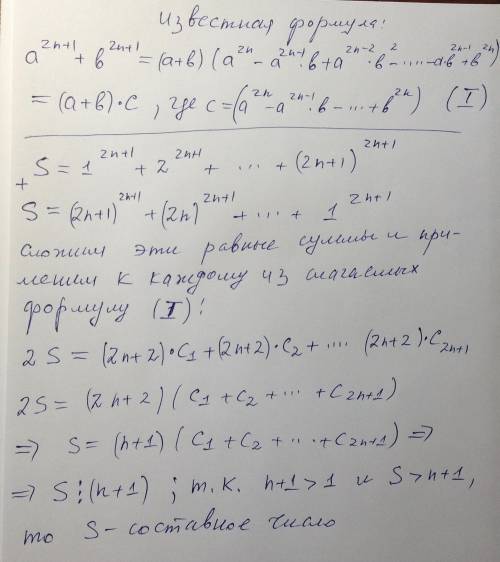
Если за час он проплавает 10 км, то сколько нужно часов, чтобы проплыть 30 км?