ответ:
пошаговое объяснения: предположим, что функциональная зависимость от не задана непосредственно , а через промежуточную величину — . тогда формулы
параметрическое представление функции одной переменной.
пусть функция задана в параметрической форме, то есть в виде:
где функции и определены и непрерывны на некотором интервале изменения параметра . найдем дифференциалы от правых и левых частей каждого из равенств:
далее, разделив второе уравнение на первое, и с учетом того, что , получим выражение для первой производной функции, заданной параметрически:
для нахождения второй производной выполним следующие преобразования:
. найти вторую производную для функции заданной параметрически.
решение. вначале находим первую производную по формуле:
производная функции по переменной равна:
производная по :
тогда
вторая производная равна
ответ.
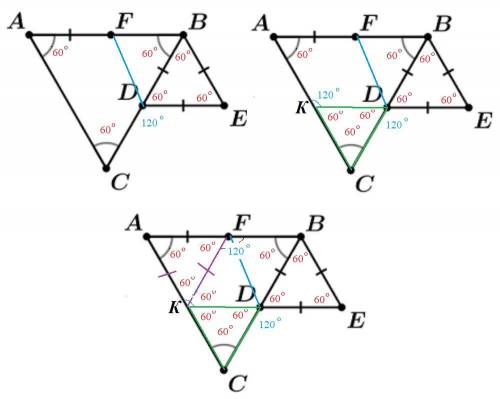
Δ АВС - равностороний ( все углы равны ∠А=∠В=∠С=60°) ⇒
АВ=ВС=АС
Δ DBE - равностороний ( все стороны равны DB=BE=DE) ⇒
∠ DBE=∠BED=∠EDB=60°
AB || DE так как внутренние накрест лежащие углы равны
∠ ABD =∠BDE=60°
∠CDE=180°-∠BDE=180°-60°=120°⇒∠CDE+∠CAD=180°
Продолжим DE до пересечения с АС в точке К
В четырехугольнике АВЕК
∠ АКЕ=360°-∠САВ-∠АВE-BED=360°-60°-(60°+60°)-60°=120°
Четырехугольник АВЕК - параллелограмм, противоположные углы равны.
⇒ BE=AK
По условию BE=AF ⇒ AK=AF и Δ AKF - равнобедренный,
с углом при вершине 60°
Значит, Δ AKF - равносторонний.
KF=AF=BE
KFBE - равнобедренная трапеция
∠ FKD=60°
∠BFK=120°
Четырехугольник KFBD - параллелограмм, противоположные углы равны.
FB=KD
FK=BD
и тогда FB=KD
О т в е т. ∠CDE+∠CAD=180°