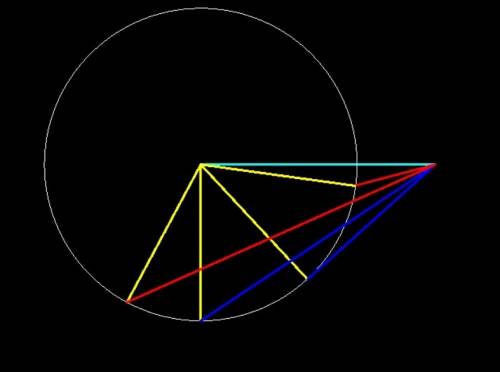
Пояснение к рисунку. Голубым цветом построен отрезок длиной 9, окружность - множество возможных положений конца отрезка длиной 6. Желтым - некоторые варианты положения отрезка длиной 6 (зеркальные не рассматриваем, чтобы не загромождать рисунок). Красным - значения а, когда треугольник становится тупоугольным (в случае малого а, тупым является угол между 6 и а, в случае большого - угол между 9 и 6). Синим цветом отрисованы граничные положения (значения а), когда
1) а становится катетом. При этом a = √9^2 - 6^2 = √81-36 = √45 = 3√5
2) а становится гипотенузой. При этом а = √9^2 + 6^2 = √81+36 = √117 = 3√13
При а между этими 2 значениями треугольник является остроугольным
3√5 < a < 3√13
1. а) 4; б) 15; в) 22; г) 8.
2. а) 3; б) 3; в) 1; г) -1,06
Пошаговое объяснение:
1. а) 4х = 16;
х = 16/4;
х = 4.
б) -15 - 3х = -7х + 45;
-3х + 7х = 45 + 15;
4х = 60;
х = 15.
в) 11 + 3х = 55 + х;
3х - 3 = 55 - 11;
2х = 44;
х = 22.
г) -3х - 17 = 8х - 105;
-3х - 8х = -105 + 17;
-11х = -88;
х = 8.
2. а) 2 * (у + 3) = 21 - 3у;
2у + 6 = 21 - 3у;
5у = 15;
у = 3.
б) -3 * (1 - 3d) - 12 = 12;
-3 + 9d = 24;
9d = 27;
d = 3.
в) -5 * (2 - 2х) = 2 * (х - 3) + 4;
-10 + 10х = 2х - 6 + 4;
8х = 8;
х = 1.
г) 0,88 - (5,12 + 0,08у) = 4,92у - у;
-4,24 - 0,08у = 3,92у;
-4у = 4,24;
у = -1,06.