Дано: y(x) = √(-x²+12*x-6)
Найти: Значения Х при минимальных значениях y(x).
1. Функция y(x) = √f(x) - существует при f(x) ≥ 0.
2. Находим точки f(x)=0 - под знаком радикала.
Решение.
1) f(x) = - x² + 12*x - 6 - функция под знаком корня.
2) Решаем квадратное уравнение f(x) = 0, находим дискриминант и корни уравнения.
D = 12² - 4*(-1)*(-6) = 144-24 = 120 - дискриминант.
√D = √120 = √(2²*30) = 2√30.
x₁ = 6 - √30, x₂ = 6 + √30 - корни квадратного уравнения. Получили область определения функции y(x):
X∈[x₁;x₂] - ООФ y(x). Минимальные значения функция на границах отрезка.
Ymin(x)=0 при x₁ = 6 - √30, x₂ = 6 + √30 - ответ.
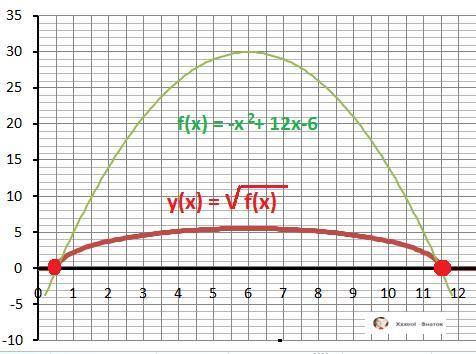
Дополнительно - графики функций - в приложении.
Максимальное значение функции y(x) равно:
Ymax(6) = √30 (≈ 5,48).
Дано: y(x) = √(-x²+12*x-6)
Найти: Значения Х при минимальных значениях y(x).
1. Функция y(x) = √f(x) - существует при f(x) ≥ 0.
2. Находим точки f(x)=0 - под знаком радикала.
Решение.
1) f(x) = - x² + 12*x - 6 - функция под знаком корня.
2) Решаем квадратное уравнение f(x) = 0, находим дискриминант и корни уравнения.
D = 12² - 4*(-1)*(-6) = 144-24 = 120 - дискриминант.
√D = √120 = √(2²*30) = 2√30.
x₁ = 6 - √30, x₂ = 6 + √30 - корни квадратного уравнения. Получили область определения функции y(x):
X∈[x₁;x₂] - ООФ y(x). Минимальные значения функция на границах отрезка.
Ymin(x)=0 при x₁ = 6 - √30, x₂ = 6 + √30 - ответ.
Дополнительно - графики функций - в приложении.
Максимальное значение функции y(x) равно:
Ymax(6) = √30 (≈ 5,48).

Пошаговое объяснение:
1) Сократить дроби означает, что нужно найти наибольший общий делитель ее числителя и знаменателя
а)6/16 , наибольший общий делитель 2
6/16=(6:2)/(16:2)=3/8
б)9/45 - общий делитель 9
9/45=(9:9)/(45:9)=1/5
в)32/88- общий делитель 8
32/88=4/11
г)(36*14)/(7*12) , разложим 36 на 6*6, 14 на 2*7, 12 на 2*6, получим
(6*6*7*2)/(7*2*6) как видим сокращаются 7,2,6, остается 6 в числителе
(36*14)/(7*12)=6
2). Сравните дроби
Чтоб сравнить дроби надо привести их к общему знаменателю
а)7/18 и 5/12 общий знаменатель 36
(7*2)/36 и (5*3)/36
14/36< 15/36, значит
7/18< 5/12
б)11/36 и 13/48, общий знаменатель 144
(11*4)/144 и (13*3)/144
44/144 >39/144, значит
11/36> 13/48