ответ: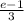
Пошаговое объяснение:
ответ: (e-1)/3
Пошаговое объяснение:
Найдём неопределённый интеграл функции e^(x^3)*x^2 чтобы использовать фундаментальную теорему исчисления.
.
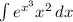Пусть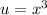 
, тогда ![x=\sqrt[3]{u}](/tpl/images/1117/3966/8c879.png)
.
![du = 3x^2dx \\ dx = \frac{du}{3x^2} = \frac{du}{3(\sqrt[3]{u} )^{2}} = \frac{du}{3u^{2/3}}](/tpl/images/1117/3966/82eee.png)
Делаем подстановку в наше изначальное выражение:
![\int{e^{x^{3}}x^2dx}=\int{e^{u}(\sqrt[3]{u})^{2}\frac{du}{3u^{2/3}} } = \int{ e^uu^{2/3}\frac{du}{3u^{2/3}} }](/tpl/images/1117/3966/640b8.png)
Здесь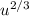 
сокращаются и мы имеем 
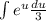. Выносим 
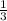за интеграл: 
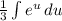. Теперь мы имеем знакомый интеграл, который равняется 
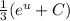, тоже самое что 
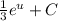. Подставляем 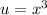и имеем 
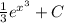. Используем фундаментальную теорему исчисления:
![\int\limits^1_0 {e^{x^3} x^2} = \frac{1}{3} e^{x^3}]_0^1=\frac{1}{3} e^{1^3}-\frac{1}{3} e^{0^3}=\frac{1}{3} e^1-\frac{1}{3} e^0=\frac{1}{3} e-\frac{1}{3}=\frac{e-1}{3}](/tpl/images/1117/3966/3089c.png)
ответ: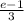
Пошаговое объяснение:
ответ: (e-1)/3
Пошаговое объяснение:
Найдём неопределённый интеграл функции e^(x^3)*x^2 чтобы использовать фундаментальную теорему исчисления.
.
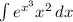Пусть 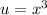, тогда .
Делаем подстановку в наше изначальное выражение:
Здесь 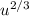сокращаются и мы имеем 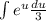. Выносим 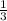за интеграл: 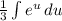. Теперь мы имеем знакомый интеграл, который равняется 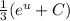, тоже самое что 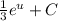. Подставляем 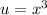и имеем 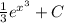. Используем фундаментальную теорему исчисления:
Д - делимое, д - делитель, Ч- частное
Д:д=Ч
Д:(2*д)=6
Д:д=12 - частное
12*3=36
Д:36=6
Д=6*36
Д=216 - делимое
216:д=12
д=216:12
д=18 - делитель
ответ: делимое - 216, делитель - 18.