Периметр треугольника равен 97 см одна из сторон а см втораяд см составте выражение для нахождения третьей стороны вычислите длину третьей стороны если а = 32 д26

👇

Увидеть ответ

Ответ:

Danika38

13.06.2022

Третья сторона равна Р-а--д=с 97-32-26=39

4,6(48 оценок)

Открыть все ответы

Ответ:

anna1866

13.06.2022

Пошаговое объяснение:

Если пешеходы шли на встречу друг другу:

4+5 = 9 (км/ч) - скорость сближения пешеходов

9*3 = 27 (км пешеходы вместе

27 - 20 = 7 (км) - расстояние между пешеходами через 3 часа (они сначала встретились, а затем разошлись)

ответ: 7 км между пешеходами через 3 часа с момента их выхода

Если пешеходы шли в противоположные стороны:

4+5 = 9 (км/ч) - скорость сближения пешеходов

9*3 = 27 (км пешеходы вместе

27 + 20 = 47 (км) - расстояние между пешеходами через 3 часа

ответ: 47 км между пешеходами через 3 часа с момента их выхода

4,4(85 оценок)

Ответ:

aikosyatb

13.06.2022

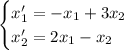
$\begin{cases} x_1'=-x_1+3x_2\\ x_2'=2x_1-x_2 \end{cases}$

Продифференцируем первое уравнение:

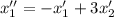
x_1''=-x_1'+3x_2'

Подставим выражение для 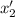x_2' :

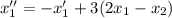
x_1''=-x_1'+3(2x_1-x_2)

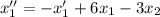
x_1''=-x_1'+6x_1-3x_2

Сложим полученное уравнение с первым уравнением системы:

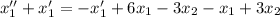
x_1''+x_1'=-x_1'+6x_1-3x_2-x_1+3x_2

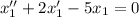
x_1''+2x_1'-5x_1=0

Составим характеристическое уравнение:

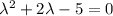
$\lambda^2+2\lambda-5=0$

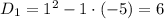
$D_1=1^2-1\cdot(-5)=6$

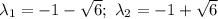
$\lambda_1=-1-\sqrt{6};\ \lambda_2=-1+\sqrt{6}$

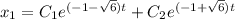
$x_1=C_1e^{(-1-\sqrt{6}) t}+C_2e^{(-1+\sqrt{6}) t}$

Найдем первую производную:

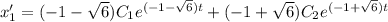
$x_1'=(-1-\sqrt{6})C_1e^{(-1-\sqrt{6}) t}+ (-1+\sqrt{6})C_2e^{(-1+\sqrt{6}) t}$

Выразим из первого уравнения 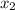x_2 :

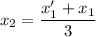
$x_2=\dfrac{x_1'+x_1}{3}$

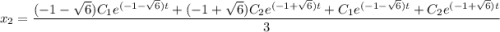
$x_2=\dfrac{(-1-\sqrt{6})C_1e^{(-1-\sqrt{6}) t}+(-1 +\sqrt{6})C_2e^{(-1+\sqrt{6}) t} +C_1e^{(-1-\sqrt{6}) t}+C_2e^{(-1+\sqrt{6}) t} }{3}$

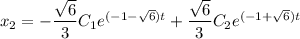
$x_2=-\dfrac{\sqrt{6}}{3}C_1e^{(-1-\sqrt{6}) t}+\dfrac{\sqrt{6}}{3}C_2e^{(-1+\sqrt{6}) t}$

Общее решение:

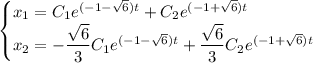
$\begin{cases} x_1=C_1e^{(-1-\sqrt{6}) t}+C_2e^{(-1+\sqrt{6}) t} \\ x_2=-\dfrac{\sqrt{6}}{3}C_1e^{(-1-\sqrt{6}) t}+\dfrac{\sqrt{6}}{3}C_2e^{(-1+\sqrt{6}) t}\end{cases}$

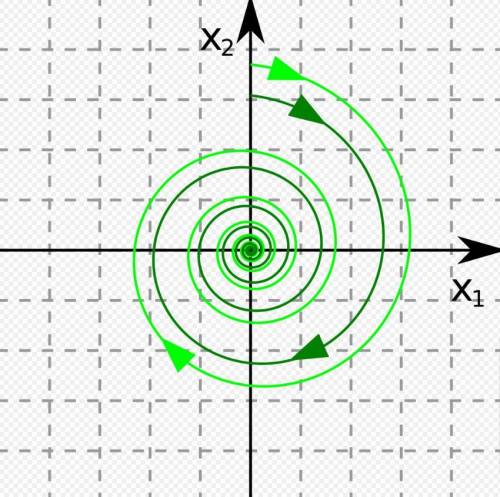
Для определения точек равновесия составим характеристическое уравнение с коэффициентами из правых частей уравнений:

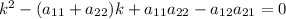
$k^2-(a_{11}+a_{22})k+a_{11}a_{22}-a_{12}a_{21}=0$

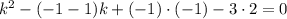
$k^2-(-1-1)k+(-1)\cdot(-1)-3\cdot2=0$

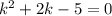
k^2+2k-5=0

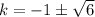
$k=-1\pm\sqrt{6}$

Так как получившиеся числа комплексные с ненулевой действительной частью, то тип точки равновесия - фокус (устойчивый фокус, так как действительная часть отрицательна).