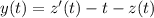
Продифференцируем второе уравнение по переменной t, получим
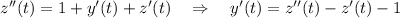
Подставляем в первое уравнение:
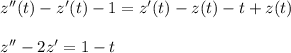
Получили линейное неоднородное дифференциальное уравнение с постоянными коэффициентами со специальной правой частью:
Найдем сначала общее решение соответствующего однородного дифференциального уравнения:
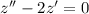
Пусть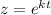 
, получим характеристическое уравнение:
Общее решение однородного дифференциального уравнения
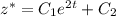
Рассмотрим полином правой части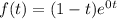 
здесь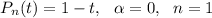 
. Сравнивая α с корнями характеристического уравнения и, принимая, во внимая что n = 0, частное решение будем искать в виде:
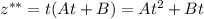
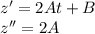
Подставляем в исходное диф. уравнение:
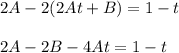
Приравниваем коэффициенты при степени t
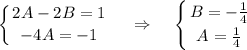
Частное решение: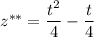 
Общее решение линейного неоднородного дифференциального уравнения:
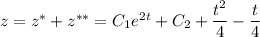
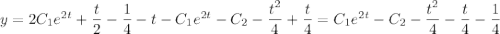
2) 240 : 48 = 5 (ч) - время в пути второго автобуса
3) 8 - 5 = 3 (ч) - на столько часов меньше был в пути второй автобус
Выражение: 304 : 38 - 240 : 48 = 3
ответ: на 3 часа меньше.