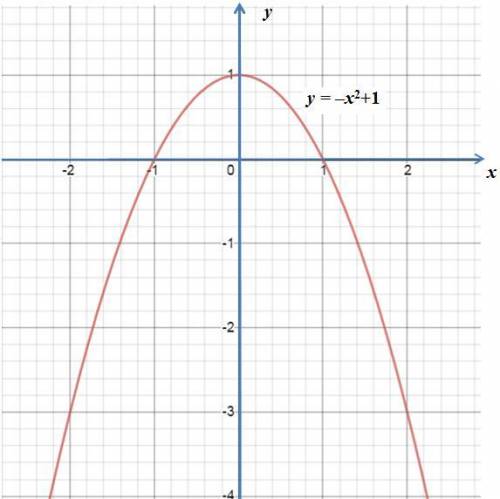
Дана функция: y = –x²+1 – парабола.
Определим абсциссу и ординату вершины параболы:
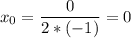
y₀ = y(x₀) = y(0) = –0²+1 = 1.
Определим нули функции:
y = 0 ⇔ –x²+1 = 0 ⇔ x² = 1 ⇔ x = ±1.
Так как перед x² коэффициент –1<0, то ветви параболы направлены вниз.
Чтобы определить, при каких значениях х функция принимает отрицательные значения, можно
использовать свойство параболы: так как y₀=1>0 и x₀=0∈[-1; 1], то на промежутке (-1; 1) функция принимает положительные значения, а в промежутках (–∞; –1) и ( 1; +∞) - отрицательные значения;
рассмотреть знак функции в промежутках (–∞; –1), (–1; 1), ( 1; +∞):
y = –x²+1 : – + –
------------------------(–1)--------------------(1)-----------------> x
Значит: в промежутках (–∞; –1) и ( 1; +∞) функция принимает отрицательные значения.
Для построения графика достаточно знать вершину и нули функции (график в приложении).
II + III = 156 р.
I + III = 132 р.
I - ? р.,
II - ? р.,
III - ? р.
Решение:
1) 156-96=60 (р.) - во II группе.
2) 96-60=36 (р) - в I группе.
3) 132-36=96 (р) - в III группе.
ответ:60,36,96
Пусть х - ряженых в первой группе
у - ряженых во второй группе
z - ряженых в третьей группе
х+y=96
y+z=156
x+z=132
Из 1 уравнения получаем х=96-у
Из 3 уравнения получаем z=156-y
Подставляем во 2 :
(96-у)+(156-у)=132
252-2у=132
2у=120
у=120:2
у=60 (р.) - во второй группе
х=96-60=36 (р.) - в первой группе
z=156-60=96 (р.) - в третьей группе
ответ: 36 ряженых в первой группе; 60 ряженых во второй группе; 96 ряженых в третьей группе