Пошаговое объяснение:
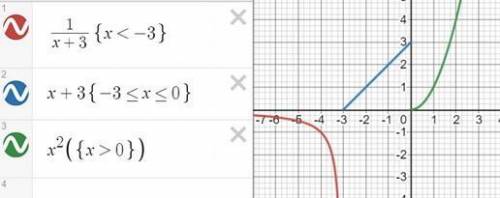
а)
точкa стыка промежутков x = -3
в точке х = -3 функция терпит разрыв. предел равен ∞, поэтому это точка разрыва II-го рода
исследуем поведение функции на отрезке (-3;0)
пределы существуют, на указанном промежутке функция непрерывна.
точка стыка промежутков x = 0
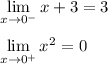
в точке х = 0 пределы существуют, но они разные, поэтому это точка разрыва I-го рода
смотрим поведение функции на отрезке (0;∞)
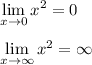
пределы существуют, функция непрерывна
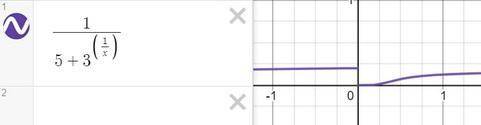
б)
для данной функции точка разрыва х = 0
исследуем ее
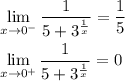
пределы существуют, но не равны, поэтому х = 0 точка разрыва I-го рода
(см. объяснение)
Пошаговое объяснение:
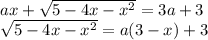
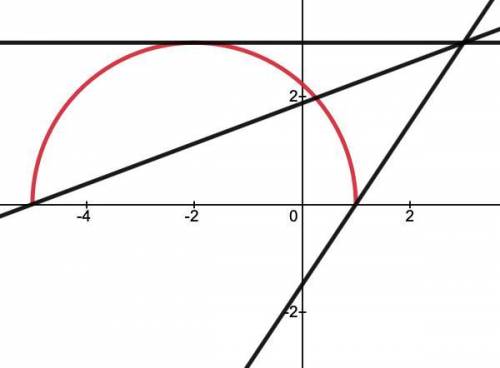
Слева видим функцию без параметра, а справа параметрическая прямая, вращающаяся вокруг точки 
. В таких случаях удобно строить отдельно левую (фиксированную) часть уравнения и правую (параметрическую) в координатах 
.
Для наглядности можно записать так:
Понятно, что в первой строке системы у нас график полуокружности, достигающий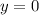 
при 
или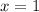 
.
После его построения будем вращать прямую вокруг точки и искать удовлетворяющие условию расположения.
(см. прикрепленный файл)
В первом случае прямая касается полуокружности в ее верхней точке, так как наибольшее значение будет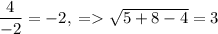 
. В этом случае 
.
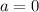Во втором случае прямая проходит через точк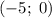и 
и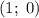 
.
Найдем соответствующие значения параметра:
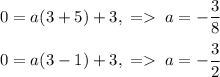
Теперь осталось только сформировать ответ:
При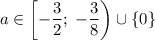 
исходное уравнение имеет ровно один корень.
Задание выполнено!
