Ще вчора побачив цікаву задачу, вирішив сьогодні розв'язати
Відповідь:
270 кг
Покрокове пояснення:
Запишемо математичну модель задачі.
х - всього цукру в магазині продано за три дні.
За ПЕРШИЙ день продано = 0,2х + 16;
Значить залишок після першого дня буде х-(0,2х+16);
За ДРУГИЙ день продано = 0,3х (х-(0,2х+16)+20=0,24х+15,2;
Залишок після другого дня буде виглядати так = х-(0,2х+16)-(0,24х+15,2);
І за ТРЕТІЙ день продано = 0,75 (х-(0,2х+16)-(0,24х+15,2)+30 = 0,75х-0,15х-12-0,18х-11,4+30 = 0,42х+6,6
Запишемо задачу рівнянням (Перший день+Другий день+Третій день=Всього):
(0,2х+16)+(0,24х+15,2)+(0,42х+6,6)=х
0,86х+37,8=х
37,8=х-0,86х
37,8=0,14х
х=37,8 : 0,14
х=270 (кг)
Перевірка:
Перший день = (270 * 20%) + 16 = 70 (кг)
Залишок на другий день 270-70=200 (кг)
Другий день = (200 * 30%) + 20 = 80 (кг)
Залишок на третій день 270-70-80=120 (кг)
Третій день = (120 * 75%) + 30 = 120 (кг)
Всього: 120+80+70=270 (кг)
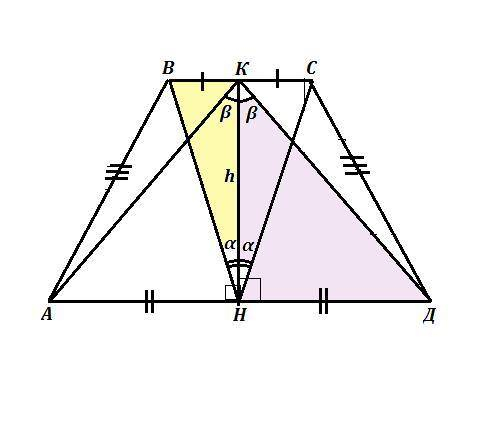
АВСД - равнобокая трапеция . АВ=СД . Высота трапеции = h .
ВК=КС , АН=НД . ∠ВНС=2α , ∠АКД=2β . Найти S .
КН - отрезок, соединяющий середины оснований трапеции.
ΔАВК=ΔДСК по 1 признаку ( АВ=СД , ВК=КС по условию, ∠В=∠С как углы в равнобедренной трапеции при основании) ⇒ АК=КД .
ΔАКН=ΔДКН по 3 признаку , так как АН=НД по усл., КН - общая , АК=КД ⇒ ∠АНК=∠ДНК=180°:2=90° , ∠АКН=∠ДКН=∠ВКД:2=2β:2=β
Поэтому КН ⊥ АД ⇒ КН=h .
Из ΔКНД : tgβ = НД/КН , tgβ = НД/h ⇒ НД = h · tgβ
Но НД=АН и АД = АН+НД = 2h · tgβ
Рассмотрим ΔВКН . Аналогично предыдущим выкладкам доказываем, что ∠ВНК = α , ∠ВКН=90° , tgα = BK/KH ⇒
BK = h · tgα ⇒ BC = BK+KC = 2h · tgα
Площадь трапеции равна
S=(AД+ВС) : 2 · КН = (2h · tgβ + 2h · tgα) : 2 · h = (h · tgβ+h · tgα) · h
S = h²· ( tgα + tgβ )
x+y=-5 ⇒ x=-5-y ⇒ x=-5-y ⇒x=-5-y
-y-x²=5 ⇒ -y-(-5-y)²=5 ⇒ -y-(25+10y+y²)=5 ⇒-y²-11y-30=0
Решим квадратное ур-ие:
-y²-11y-30=0 |·(-1)
y²+11y+30=0
a=1,b=11,c=30
D=b²-4ac=121-120=1
y₁=-b+√D/2a=-11+1/2=-5
y₂=-b-√D/2a=-11-1/2=-6
Подставим значения y под ур-ие x=-5-y из системы:
x=-5-y ⇒x₁=-5+5=0
x₂=-5+6=1
ответ:y₁=-5,y₂=-6,x₁=0,x₂=1