То, что решается через характеристическое уравнение - это общее решение. Оно всегда будет независимо от правой части диффура.
По сути, нужно найти так называемое частное решение, и тогда решением для этого диффура будет сумма общего и частного решений.
Частное решение подбирается, исходя из правой части. В данном случае, правая часть есть многочлен второго порядка. Поэтому частное решение будет также иметь вид многочлена, причем многочлена второго порядка: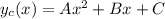 
(
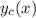- частное решение, A, B и C - константы, которые нужно подобрать). Теперь необходимо подставить это решение вместо y в данном диффуре, и найти константы.
(второго порядка потому, что многочлена первого порядка может не хватать, а многочлен не ниже третьего порядка избыточен, можешь попробовать подставить многочлен третьего порядка, но при нахождении коэффициентов он занулится)
UPD: ошибся в выборе многочена. Нужно использовать многочлен третьего порядка: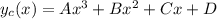 
(необходимо, чтобы после подстановки 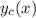в диффур в левой части получился многочлен не ниже порядка многочлена в правой части)
Поскольку известны корни трехчлена, то верны следующие равенства:
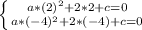
Преобразовываем оба уравнения:
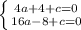
Вычитаем второе из первого:
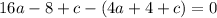
Приводим подобные:
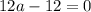, отсюда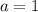 
Подставляем a в одно из уравнений, например, в первое:
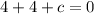, откуда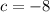 
Тогда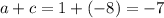 
По теореме Виета, для квадратного уравнения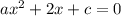 
, если 
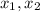- корни уравнения, то верно следующее:
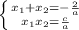
(правая часть первого уравнения - коэффициент при x, деленный на коэффициент при старшей степени, т.е. a, взятый со знаком минус, правая часть второго уравнения - свободный коэффициент, то бишь c, деленный на коэффициент при старшей степени, то бишь a)
Поскольку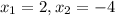 
, то получаем:
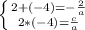
Из первого уравнения находим 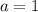. Подставляем a во второе уравнение, находим, что 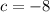. Наконец, находим сумму:
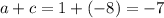
Эпилог
Двумя получили одинаковый результат, и это хорошо.
24+8=32
ответ:32