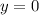 является решением уравнения. Разделим обе части на
является решением уравнения. Разделим обе части на 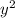 , предполагая, что
, предполагая, что 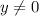 :
: .
.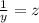 , тогда
, тогда 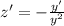 и уравнение принимает вид
и уравнение принимает вид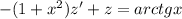 .
.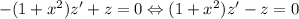 .
.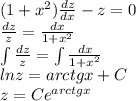 .
.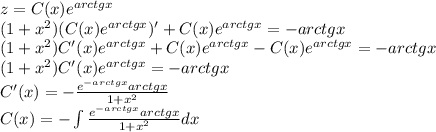 .
.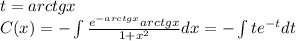 .
.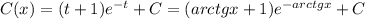 , где C - произвольная постоянная.
, где C - произвольная постоянная.
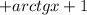 .
.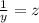 , тогда
, тогда 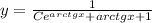 - общее решение.
- общее решение.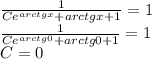 .
.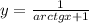 .
.
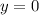 является решением уравнения. Разделим обе части на
является решением уравнения. Разделим обе части на 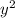 , предполагая, что
, предполагая, что 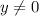 :
: .
.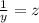 , тогда
, тогда 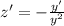 и уравнение принимает вид
и уравнение принимает вид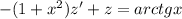 .
.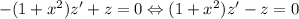 .
.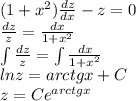 .
.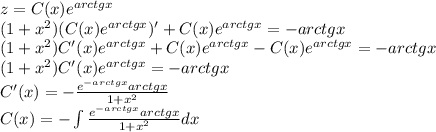 .
.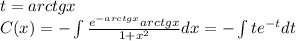 .
.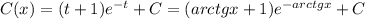 , где C - произвольная постоянная.
, где C - произвольная постоянная.
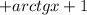 .
.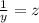 , тогда
, тогда 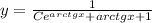 - общее решение.
- общее решение.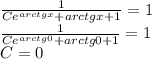 .
.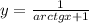 .
.
АБВГ
+АБДГ
ВГДАГ
Поскольку Г+Г=Г, то Г=0.
4-х значное прибавляют к 4-хзначному в итоге получается пятизначное число. Значит ВГ=10.
Поскольку А+А=10, то А=5.
В+Д=А, А=5, А=1 ⇒ Д=4
Б+Б=Д ⇒ Б=Д:2 ⇒Б=2
Получаем 5210+5240=10450